题目内容
对于定义域分别为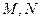 的函数
的函数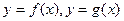 ,规定:
,规定:
函数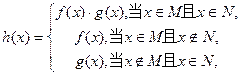
(1) 若函数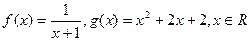 ,求函数
,求函数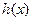 的取值集合;
的取值集合;
(2) 若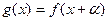 ,其中
,其中 是常数,且
是常数,且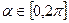 ,请问,是否存在一个定义域为
,请问,是否存在一个定义域为 的函数
的函数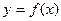 及一个
及一个 的值,使得
的值,使得 ,若存在请写出一个
,若存在请写出一个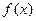 的解析式及一个
的解析式及一个 的值,若不存在请说明理由。
的值,若不存在请说明理由。
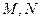 的函数
的函数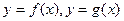 ,规定:
,规定:函数
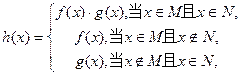
(1) 若函数
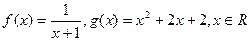 ,求函数
,求函数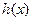 的取值集合;
的取值集合;(2) 若
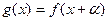 ,其中
,其中 是常数,且
是常数,且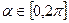 ,请问,是否存在一个定义域为
,请问,是否存在一个定义域为 的函数
的函数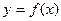 及一个
及一个 的值,使得
的值,使得 ,若存在请写出一个
,若存在请写出一个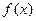 的解析式及一个
的解析式及一个 的值,若不存在请说明理由。
的值,若不存在请说明理由。 解(1)由函数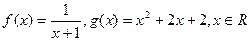
可得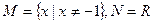
从而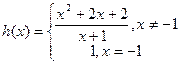 ……………………………………………..2分
……………………………………………..2分
当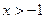 时,
时,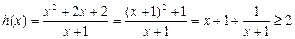 …………………….4分
…………………….4分
当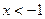 时,
时,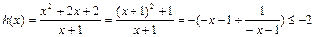 …………….6分
…………….6分
所以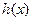 的取值集合为
的取值集合为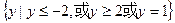 ………………….7分
………………….7分
(2)由函数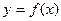 的定义域为
的定义域为 ,得
,得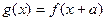 的定义域为
的定义域为
所以,对于任意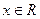 ,都有
,都有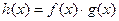
即对于任意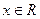 ,都有
,都有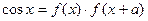
∴我们考虑将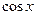 分解成两个函数的乘积,而且这两个函数还可以通过平移相互转化
分解成两个函数的乘积,而且这两个函数还可以通过平移相互转化

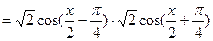
所以,令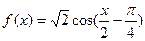 ,且
,且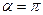 ,即可 ………………………………..14分
,即可 ………………………………..14分
又
所以,令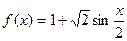 ,且
,且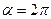 ,即可(答案不唯一)
,即可(答案不唯一)
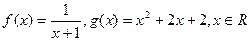
可得
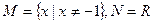
从而
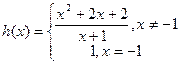 ……………………………………………..2分
……………………………………………..2分当
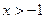 时,
时,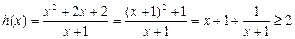 …………………….4分
…………………….4分当
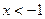 时,
时,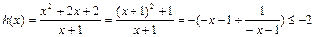 …………….6分
…………….6分所以
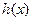 的取值集合为
的取值集合为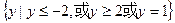 ………………….7分
………………….7分(2)由函数
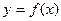 的定义域为
的定义域为 ,得
,得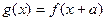 的定义域为
的定义域为
所以,对于任意
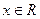 ,都有
,都有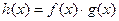
即对于任意
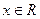 ,都有
,都有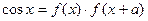
∴我们考虑将
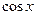 分解成两个函数的乘积,而且这两个函数还可以通过平移相互转化
分解成两个函数的乘积,而且这两个函数还可以通过平移相互转化
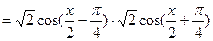
所以,令
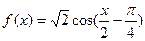 ,且
,且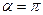 ,即可 ………………………………..14分
,即可 ………………………………..14分又

所以,令
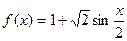 ,且
,且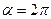 ,即可(答案不唯一)
,即可(答案不唯一)略

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
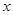 ,有
,有 ,
, 时
时



 的两个函数
的两个函数 ,对于任意的
,对于任意的 满足:
满足: 且
且
 的值并分别写出一个
的值并分别写出一个 和
和 的解析式,使它们满足已知条件(不要求说明理由)
的解析式,使它们满足已知条件(不要求说明理由) ,记
,记
 , 求证:
, 求证: 
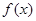 满足
满足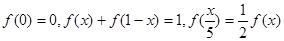 ,且当
,且当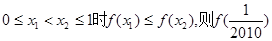 等于( )
等于( )



 ,若对于任意
,若对于任意 ,总存在
,总存在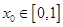 ,使得
,使得 成立,则
成立,则 的 取值范围是 ▲ .
的 取值范围是 ▲ . 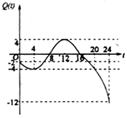
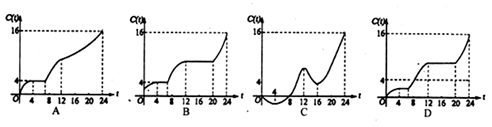
 满足
满足 ,且
,且 。
。 上,
上,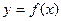 的图象恒在
的图象恒在 的图象上方,试确定实数
的图象上方,试确定实数 的范围。
的范围。 则
则 =" " ;
=" " ;