题目内容
若复数z满足|z+4+3i|=3，则复数z的模应满足的不等式是（ ）
| A．5≤|z|≤8 | B．2≤|z|≤8 | C．|z|≤5 | D．|z|＜8 |
设z=x+yi（x，y∈R），
∵|z+4+3i|=3
∴（x+4）2+（y+3）2=9，
则（x，y）点表示以（-4，3）为圆心，以3为半径的圆
而复数|Z|=
表示（x，y）点到原点的距离，
由于（-4，3）到原点的距离为5，
故5-3≤|Z|≤5+3
即2≤|Z|≤8
故选B
∵|z+4+3i|=3
∴（x+4）2+（y+3）2=9，
则（x，y）点表示以（-4，3）为圆心，以3为半径的圆
而复数|Z|=
| x2+y2 |
由于（-4，3）到原点的距离为5，
故5-3≤|Z|≤5+3
即2≤|Z|≤8
故选B
练习册系列答案
相关题目
若复数z满足|z+4+3i|=3，则复数z的模应满足的不等式是（ ）
| A、5≤|z|≤8 | B、2≤|z|≤8 | C、|z|≤5 | D、|z|＜8 |
=（ ）
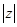C．
D．