题目内容
已知PA,PB,PC两两互相垂直,且△PAB、△PAC、△PBC的面积分别为1.5cm2,2cm2,6cm2,则过P,A,B,C四点的外接球的表面积为 cm2.(注S球=4πr2,其中r为球半径)
【答案】分析:当三线互相垂直时,联想构造长方体.长方体的对角线即为外接球的直径.求出半径,即可求出外接球的表面积.
解答:解:设PA,PB,PC分别为a,b,c,PA,PB,PC两两互相垂直,扩展为长方体,它的外接球的直径就是,长方体的体对角线的长,
由题意可知:ab=3,ac=4,bc=12,所以a=1,b=3,c=4,所以长方体的体对角线的长为: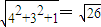
所以取得半径为: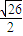 ,
,
球的表面积:4πr2=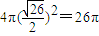 (cm2)
(cm2)
故答案为:26π
点评:本题考查球的表面积,长方体的外接球的知识,考查计算能力,逻辑思维能力,是基础题.
解答:解:设PA,PB,PC分别为a,b,c,PA,PB,PC两两互相垂直,扩展为长方体,它的外接球的直径就是,长方体的体对角线的长,
由题意可知:ab=3,ac=4,bc=12,所以a=1,b=3,c=4,所以长方体的体对角线的长为:
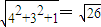
所以取得半径为:
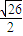 ,
,球的表面积:4πr2=
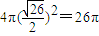 (cm2)
(cm2)故答案为:26π
点评:本题考查球的表面积,长方体的外接球的知识,考查计算能力,逻辑思维能力,是基础题.

练习册系列答案
相关题目