题目内容
设函数f(x)=A.(-∞,1) B.(0,1) C.(1,+∞) D.[1,+∞)
解析:y=f(x)=![]() =
=![]() =1+
=1+![]() .
.
当a<1时,图象如图1所示;
当a>1时,图象如图2所示.
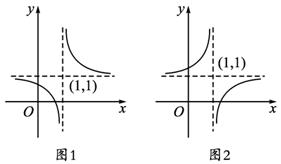
由图象可知,a>1时,函数y在(1,+∞)上为增函数,此时f′(x)>0,同时f(x)<0的解集为(1,+∞)的真子集.故选C.
答案:C

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
题目内容
设函数f(x)=A.(-∞,1) B.(0,1) C.(1,+∞) D.[1,+∞)
解析:y=f(x)=![]() =
=![]() =1+
=1+![]() .
.
当a<1时,图象如图1所示;
当a>1时,图象如图2所示.

由图象可知,a>1时,函数y在(1,+∞)上为增函数,此时f′(x)>0,同时f(x)<0的解集为(1,+∞)的真子集.故选C.
答案:C

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案