题目内容
2.求等腰直角三角形中两直角边上的中线所成的钝角的余弦值.分析 设在等腰直角三角形ABC中,∠C=90°,中线AD与BE相交于O,则∠CAD=∠CBE,∠AOB=90°+2∠CAD,由此能求出等腰直角三角形中两直角边上的中线所成的钝角的余弦值.
解答  解:设在等腰直角三角形ABC中,∠C=90°,
解:设在等腰直角三角形ABC中,∠C=90°,
中线AD与BE相交于O,则∠CAD=∠CBE,
∠AOB=∠CBE+∠ODB=∠CBE+∠CAD+∠C=90°+2∠CAD,
在Rt△CAD中,设CD=1,则BC=2,∴AD=$\sqrt{5}$,
∴sin∠CAD=$\frac{1}{\sqrt{5}}$,cos∠CAD=$\frac{2}{\sqrt{5}}$,
∴cos∠AOB=cos(90°+2∠CAD)=-sin2∠CAD
=-2sin∠CAD•cos∠CAD
=-2×$\frac{1}{\sqrt{5}}$×$\frac{2}{\sqrt{5}}$
=-$\frac{4}{5}$.
∴等腰直角三角形中两直角边上的中线所成的钝角的余弦值为-$\frac{4}{5}$.
点评 本题考查等腰直角三角形中两直角边上的中线所成的钝角的余弦值的求法,是中档题,解题时要认真审题,注意三角形诱导公式、正弦二倍角公式的合理运用.

练习册系列答案
相关题目
14.直线x-y+2=0与圆$\left\{\begin{array}{l}x=2cosθ\\ y=2sinθ\end{array}\right.$(θ为参数)的位置关系是( )
| A. | 相离 | B. | 相切 | ||
| C. | 直线过圆心 | D. | 相交但直线不过圆心 |
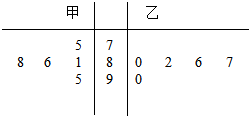 如图是甲乙两同学在高三的五次月考成绩的茎叶图,对甲乙的考试成绩作比较,请你写出两个统计结论:
如图是甲乙两同学在高三的五次月考成绩的茎叶图,对甲乙的考试成绩作比较,请你写出两个统计结论: