题目内容
双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直l1的直线分别交l1,l2于A,B两点,己知|| OA |
| AB |
| OB |
| BF |
| FA |
分析:由2个向量同向,得到渐近线的夹角范围,求出离心率的范围,再用勾股定理得出直角三角形的2个直角边的长度比,联想到渐近线的夹角,求出渐近线的斜率,进而求出离心率.
解答:解:设双曲线方程为
-
=1,c2=a2+b2由
,
同向,
∴渐近线的倾斜角为(0,
),
∴渐近线斜率为:k1=
<1∴
=
=e2-1<1,∴1<e2<2
∴|AB|2=(|OB|-|OA|)(|OB|+|OA|)=(|OB|-|OA|)2|AB|,
∴|AB|=2(|OB|-|OA|)∴
∴|OA|=
|AB|∴|OA|2=
|AB|2
可得:
=
,而在直角三角形OAB中,
注意到三角形OAF也为直角三角形,即tan∠AOB=
而由对称性可知:OA的斜率为k=tan(
-
∠AOB)
∴
=
,∴2k2+3k-2=0,∴k=
(k=-2舍去);
∴
=
∴
=
=
,∴e2=
∴e=
故答案为
.
| x2 |
| a2 |
| y2 |
| b2 |
| BF |
| FA |
∴渐近线的倾斜角为(0,
| π |
| 4 |
∴渐近线斜率为:k1=
| b |
| a |
| b2 |
| a2 |
| c2-a2 |
| a2 |
∴|AB|2=(|OB|-|OA|)(|OB|+|OA|)=(|OB|-|OA|)2|AB|,
∴|AB|=2(|OB|-|OA|)∴
|
∴|OA|=
| 3 |
| 4 |
| 9 |
| 16 |
可得:
| |AB| |
| |OA| |
| 4 |
| 3 |
注意到三角形OAF也为直角三角形,即tan∠AOB=
| 4 |
| 3 |
而由对称性可知:OA的斜率为k=tan(
| π |
| 2 |
| 1 |
| 2 |
∴
| 2k |
| 1-k2 |
| 4 |
| 3 |
| 1 |
| 2 |
∴
| b |
| a |
| 1 |
| 2 |
| b2 |
| a2 |
| c2-a2 |
| a2 |
| 1 |
| 4 |
| 5 |
| 4 |
∴e=
| ||
| 2 |
故答案为
| ||
| 2 |
点评:本题考查了双曲线的简单性质以及等差数列的性质,做到边做边看,从而发现题中的巧妙,如据
=
,联想到对应的是渐近线的夹角的正切值,是解题的关键.
| |AB| |
| |OA| |
| 4 |
| 3 |

练习册系列答案
相关题目
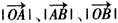 成等差数列,且
成等差数列,且 与
与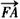 同向,
同向,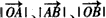 成等差数列,且
成等差数列,且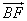 与
与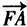 同向。
同向。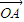 |、|
|、|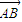 |、|
|、|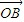 |成等差数列,且
|成等差数列,且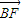 与
与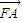 同向.
同向.