题目内容
函数 的图象为C1,C1关于点A(2,1)的对称图形为C2,C2对应的函数为g(x):
的图象为C1,C1关于点A(2,1)的对称图形为C2,C2对应的函数为g(x):
(1)求函数g(x)的解析式;
(2)若直线y=b与C2只有一个公共点,求b的值及交点坐标.
解:(1)函数g(x)图象任一点P(x,y),且P关于A(2,1)的对称点P'(x',y'),
则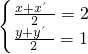 ,解得
,解得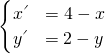 ,
,
∵点P'在函数 的图象上,∴2-y=
的图象上,∴2-y=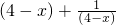 ,
,
即g(x)=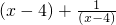 +2.
+2.
(2)当x-4>0时,即x>4,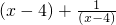 ≥2,当且仅当x=5时取到等号,
≥2,当且仅当x=5时取到等号,
此时g(x)取到最小值4,
∵直线y=b与C2只有一个公共点,∴b=4,且交点坐标是(5,4);
当x-4<0时,即x<4,-[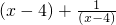 ]≥2,即
]≥2,即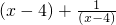 ≤-2,
≤-2,
此时g(x)取到最大值0,当且仅当x=3时取到等号
∵直线y=b与C2只有一个公共点,∴b=0,且交点坐标是(3,0);
综上,b的值及交点坐标分别为4,(5,4)或0,(3,0).
分析:(1)先设g(x)图象任一点P(x,y)以及P关于A(2,1)的对称点P'(x',y'),根据点关于点对称的性质,用p的坐标表示P'的坐标,再把P'的坐标代入f(x)的解析式进行整理,求出g(x)解析式;
(2)需要对x进行分类后,利用基本不等式求出函数g(x)的最值,再由条件和等号取到的条件求出b的值和交点的坐标.
点评:本题是有关函数的综合题,考查了用代入法求函数的解析式,利用点关于点对称的性质,还利用基本不等式求出函数的最值,注意基本不等式的使用条件,考查了分类讨论思想.
则
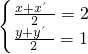 ,解得
,解得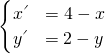 ,
,∵点P'在函数
 的图象上,∴2-y=
的图象上,∴2-y=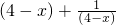 ,
,即g(x)=
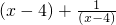 +2.
+2.(2)当x-4>0时,即x>4,
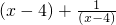 ≥2,当且仅当x=5时取到等号,
≥2,当且仅当x=5时取到等号,此时g(x)取到最小值4,
∵直线y=b与C2只有一个公共点,∴b=4,且交点坐标是(5,4);
当x-4<0时,即x<4,-[
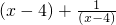 ]≥2,即
]≥2,即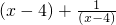 ≤-2,
≤-2,此时g(x)取到最大值0,当且仅当x=3时取到等号
∵直线y=b与C2只有一个公共点,∴b=0,且交点坐标是(3,0);
综上,b的值及交点坐标分别为4,(5,4)或0,(3,0).
分析:(1)先设g(x)图象任一点P(x,y)以及P关于A(2,1)的对称点P'(x',y'),根据点关于点对称的性质,用p的坐标表示P'的坐标,再把P'的坐标代入f(x)的解析式进行整理,求出g(x)解析式;
(2)需要对x进行分类后,利用基本不等式求出函数g(x)的最值,再由条件和等号取到的条件求出b的值和交点的坐标.
点评:本题是有关函数的综合题,考查了用代入法求函数的解析式,利用点关于点对称的性质,还利用基本不等式求出函数的最值,注意基本不等式的使用条件,考查了分类讨论思想.

练习册系列答案
相关题目
 已知函数
已知函数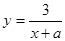 的图象C向左平移一个单位后,得到y=
的图象C向左平移一个单位后,得到y=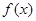 的图象C1,若曲线C1关于原点对称,那么实数a的的值为( )A.1 B.-1 C.0 D.-3
的图象C1,若曲线C1关于原点对称,那么实数a的的值为( )A.1 B.-1 C.0 D.-3