题目内容
已知f-1(x)是f(x)=1-3x的反函数,p:|f-1(a)|<2;q:{x|x2+(a+2)x+1=0,x∈R}∩{x|x>0}=
解析:∵f(x)=1-3x,∴f-1(x)=![]() .
.
由f-1(a)|<2得|![]() |<2,
|<2,
∴-5<a<7.
由q![]() Δ(a+2)2-4<0
Δ(a+2)2-4<0
或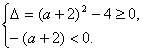
![]() -4<a<0或a≥0
-4<a<0或a≥0![]() a>-4.
a>-4.
p或q为真,p且q为假,则p、q一真一假,
∴-5<a≤-4或a≥7.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
题目内容
已知f-1(x)是f(x)=1-3x的反函数,p:|f-1(a)|<2;q:{x|x2+(a+2)x+1=0,x∈R}∩{x|x>0}=
解析:∵f(x)=1-3x,∴f-1(x)=![]() .
.
由f-1(a)|<2得|![]() |<2,
|<2,
∴-5<a<7.
由q![]() Δ(a+2)2-4<0
Δ(a+2)2-4<0
或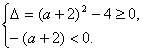
![]() -4<a<0或a≥0
-4<a<0或a≥0![]() a>-4.
a>-4.
p或q为真,p且q为假,则p、q一真一假,
∴-5<a≤-4或a≥7.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案