题目内容
连接球面上任意两点的线段称为球的弦，已知半径为5的球上有两条长分别为6和8的弦，则此两弦中点距离的最大值是分析：将球的问题转化为球的大圆的问题解决，为使两弦中点距离的最大值，画出同时包含两条长分别为6和8的弦，它们必定平行，再利用圆中线段求解即可．
解答：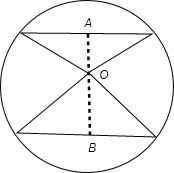
解：如图，是球的一个大圆，其包含了两条平行的弦，
由圆中线段的关系，得：
OA=
=4，
OB=
=3，
∵题目中要求的是最大值，只有在球心的不同侧一种情况，
∴两弦中点距离的最大值是7．
故填：7．
解：如图，是球的一个大圆，其包含了两条平行的弦，由圆中线段的关系，得：
OA=
| 52-32 |
OB=
| 52-42 |
∵题目中要求的是最大值，只有在球心的不同侧一种情况，
∴两弦中点距离的最大值是7．
故填：7．
点评：本题主要考查了球的性质，对于球的问题，最关键的元素是球心和球的大圆，利用这两点，可将立体几何问题转化为平面几何问题解决．
练习册系列答案
相关题目