题目内容
成都市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰。若现有500人参加测试,学生成绩的频率分布直方图如下:

(I)求获得参赛资格的人数;
(II)根据频率直方图,估算这500名学生测试的平均成绩;
(III)若知识竞赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛,已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为 ,求甲在初赛中答题个数的分布列及数学期望.
,求甲在初赛中答题个数的分布列及数学期望.

(I)求获得参赛资格的人数;
(II)根据频率直方图,估算这500名学生测试的平均成绩;
(III)若知识竞赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛,已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为
 ,求甲在初赛中答题个数的分布列及数学期望.
,求甲在初赛中答题个数的分布列及数学期望.(I) 125;(II)78.48;(III) 分布列为:
数学期望为 .
.
 | 3 | 4 | 5 |
 | 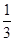 |  |  |
 .
.试题分析:(I)将频率分布直方图中90~150的小矩形的面积相加,便得获得参赛资格的人数的频率.频率乘以测试总人数500,便得获得参赛资格的人数.
(II)在频率分布直方图中,平均值等于每小组的频率乘以每小组中点的值的和.
(III)已知连续两次答错的概率为
 ,由此可得答对每一道题的概率.注意,答题的个数
,由此可得答对每一道题的概率.注意,答题的个数 包括答对的和答错的.显然答题的个数
包括答对的和答错的.显然答题的个数 可取3、4、5. “
可取3、4、5. “ ”表示连续答对3个或连续答错3个;“
”表示连续答对3个或连续答错3个;“ ”表示前3题中恰好答对2个且第4 个题答对或前3题中恰好答错2个且第4 个题答错;“
”表示前3题中恰好答对2个且第4 个题答对或前3题中恰好答错2个且第4 个题答错;“ ”表示前4个题恰好答对2个.根据独立事件的概率公式便可得
”表示前4个题恰好答对2个.根据独立事件的概率公式便可得  的分布列,由随机变量的数学期望公式可求得
的分布列,由随机变量的数学期望公式可求得 的期望.
的期望. 试题解析:(I)获得参赛资格的人数
 2分
2分(II)平均成绩:

 5分
5分(III)设甲答对每一道题的概率为.P
则



 的分布列为
的分布列为 | 3 | 4 | 5 |
 | 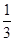 |  |  |
 12分
12分
练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 (单位:
(单位: )表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.
)表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.





 年
年 月份的
月份的 天中随机抽取
天中随机抽取 天的
天的
 个,设
个,设 为空气质量类别为优或良的天数,求
为空气质量类别为优或良的天数,求


 ,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的
,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的 大小为多少?并说明
大小为多少?并说明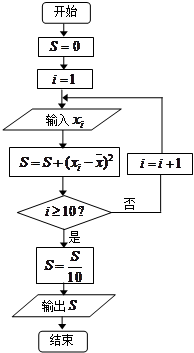



 名编号为
名编号为 的球员进行足球点球练习,每人点球
的球员进行足球点球练习,每人点球 次,射中的次数如下表:
次,射中的次数如下表: .
.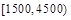 元之间,根据调查结果得出职工的月收入情况残缺的频率分布直方图如图(图左)所示,则该单位职工的月收入的平均数大约是 元.
元之间,根据调查结果得出职工的月收入情况残缺的频率分布直方图如图(图左)所示,则该单位职工的月收入的平均数大约是 元.
 名高三学生期中考试数学成绩的频率分布直方图如图所示,由图中数据估计此次数学成绩平均分为( )
名高三学生期中考试数学成绩的频率分布直方图如图所示,由图中数据估计此次数学成绩平均分为( )



