题目内容
在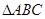 中,角
中,角 ,
, ,
, 的对边为
的对边为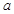 ,
,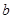 ,
,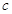 且;
且;
(Ⅰ)求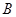 的值;
的值;
(Ⅱ)若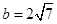 ,
,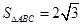 ,求
,求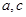 的值.
的值.
【答案】
(Ⅰ)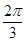 ;(Ⅱ)
;(Ⅱ)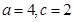 或者
或者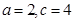
【解析】
试题分析:(Ⅰ)因为在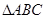 中,角
中,角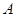 ,
,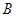 ,
,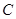 的对边为
的对边为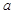 ,
,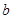 ,
,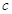 且;
且;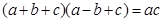 通过化简,可得三角形三边的关系,结合余弦定理即可求出结论.
通过化简,可得三角形三边的关系,结合余弦定理即可求出结论.
(Ⅱ)由三角形的面积公式即可得到一个关于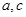 的等式,又由前题可得
的等式,又由前题可得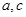 的关系式,通过解关于
的关系式,通过解关于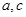 的方程即可求得结论.本题的关键就是应用三角形的余弦定理即三角形的面积公式.还有就是通过整体性解方程的思维.
的方程即可求得结论.本题的关键就是应用三角形的余弦定理即三角形的面积公式.还有就是通过整体性解方程的思维.
试题解析:(Ⅰ)由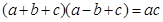 可得
可得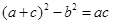 ,所以
,所以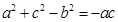 .所以
.所以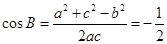 . 又
. 又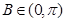 ,所以
,所以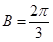 .
.
(Ⅱ)由(Ⅰ)可知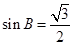 ,所以
,所以 .可得
.可得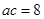 .又由
.又由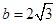 以及余弦定理
以及余弦定理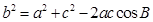 可知
可知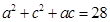 ,即
,即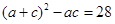 ,又
,又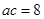 代入可得
代入可得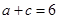 .又由
.又由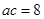 可得
可得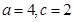 或者
或者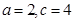 .
.
考点:1.余弦定理.2.三角形的面积.3.二元二次的方程组的思想.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
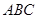 中,角
中,角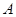 、
、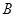 、
、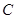 的对边分别为
的对边分别为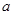 、
、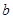 、
、 ,已知
,已知 ,
,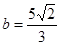 ,
,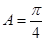 ,则
,则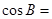 。
。 中,角
中,角 、
、 、
、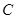 的对边分别为
的对边分别为 ,若
,若 ,且
,且 .
.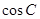 的值;
(2)若
的值;
(2)若 ,求△
,求△ 中,角
中,角 ,
, ,
, 的对边的边长分别为
的对边的边长分别为 ,
, ,
, ,且
,且
 .
. 的大小;
的大小; ;②
;② ;③
;③ .
.