题目内容
设定义在R上的函数 若关于
若关于 的方程
的方程 有9个不同实数解,则实数
有9个不同实数解,则实数 的取值范围是( )
的取值范围是( )
| A.(0,1) | B. |
C. | D. |
D
解析

练习册系列答案
相关题目
设函数 的定义域为
的定义域为 ,若对于任意
,若对于任意 且
且 ,恒有
,恒有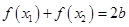 ,则称点
,则称点 为函数
为函数 图象的对称中心.研究并利用函数
图象的对称中心.研究并利用函数 的对称中心,可得
的对称中心,可得 ( )
( )
| A.4023 | B.-4023 | C.8046 | D.-8046 |
设函数f(x)是定义在R上的奇函数,且f(-3)=-2,则f(3)+f(0)=( )
| A.3 | B.-3 | C.2 | D.7 |
若函数 的定义域是
的定义域是 ,则函数
,则函数 的定义域是
的定义域是
A. | B. | C. | D. |
下列四组函数是同一函数的个数为
(1) 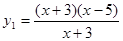 ,
,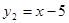 ; (2)
; (2) 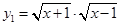 ,
,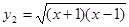
(3)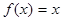 ,
,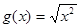 ; (4)
; (4)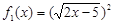 ,
,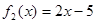
| A.0 | B.1 | C.2 | D. 3 |
已知函数 为奇函数,则
为奇函数,则 ( )
( )
A. | B. | C.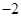 | D. |
若奇函数 在
在 上是增函数,且最小值是1,则它在
上是增函数,且最小值是1,则它在 上是( )
上是( )
| A.增函数且最小值是-1 | B.增函数且最大值是-1 |
| C.减函数且最大值是-1 | D.减函数且最小值是-1 |
已知函数f(x)的定义域为[-3,+∞),且f(6)=2。f′(x)为f(x)的导函数,f′(x)的图象如图所示.若正数a,b满足f(2a+b)<2,则 的取值范围是( )
的取值范围是( )
A. ∪(3,+∞) ∪(3,+∞) | B. |
C. ∪(3,+∞) ∪(3,+∞) | D. |
 表示一个圆
表示一个圆 则( )
则( )






