题目内容
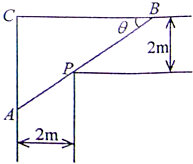 某直角走廊的示意图如图所示,其两边走廊的宽度均为2m.
某直角走廊的示意图如图所示,其两边走廊的宽度均为2m.(1)过点p的一条直线与走廊的外侧两边交于A,B两点,且与走廊的一边的夹角为θ(0<θ<
| π | 2 |
(2)一根长度为5m的铁棒能否水平(铁棒与地面平行)通过该直角走廊?请说明理由(铁棒的粗细忽略不计).
分析:(1)根据图可知l(θ)=BP+AP,而BP=
,AP=
代入整理可得函数.
(2)“长度为5m的铁棒能否水平(铁棒与地面平行)通过该直角走廊,铁棒能水平通过该直角直廊”,关键看函数l(θ)=的值域,先研究其单调性,用导数法,先求导,令l'(θ)=0得,θ=
,易知当0<θ<
时,l'(θ)<0,l(θ)为减函数;当
<θ<
时,l'(θ)>0,l(θ)为增函数,可知当θ=
时,l(θ)有最小值,再与5比较得到结论.
| 2 |
| sinθ |
| 2 |
| cosθ |
(2)“长度为5m的铁棒能否水平(铁棒与地面平行)通过该直角走廊,铁棒能水平通过该直角直廊”,关键看函数l(θ)=的值域,先研究其单调性,用导数法,先求导,令l'(θ)=0得,θ=
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
解答:解:(1)根据图得:l(θ)=BP+AP=
+
,θ∈(0,
).
(2)铁棒能水平通过该直角直廊,
理由如下:l′(θ)=(
)′+(
)′
=
+
=
.
令l'(θ)=0得,θ=
.
当0<θ<
时,l'(θ)<0,l(θ)为减函数;
当
<θ<
时,l'(θ)>0,l(θ)为增函数;
所以当θ=
时,l(θ)有最小值4
,
因为4
>5,所以铁棒能水平通过该直角走廊.
| 2 |
| sinθ |
| 2 |
| cosθ |
| π |
| 2 |
(2)铁棒能水平通过该直角直廊,
理由如下:l′(θ)=(
| 2 |
| sinθ |
| 2 |
| cosθ |
=
| 0•sinθ-2•cosθ |
| sin2θ |
| 0•cosθ+2•sinθ |
| cos2θ |
| 2(sin2θ-cos2θ) |
| sin2θcos2θ |
令l'(θ)=0得,θ=
| π |
| 4 |
当0<θ<
| π |
| 4 |
当
| π |
| 4 |
| π |
| 2 |
所以当θ=
| π |
| 4 |
| 2 |
因为4
| 2 |
点评:本题主要考查函数模型的建立与应用,还考查了三角函数的定义,导数法求函数最值等.

练习册系列答案
相关题目
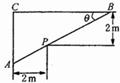 某直角走廊的示意图如图所示,其两边走廊的宽度均为2m.
某直角走廊的示意图如图所示,其两边走廊的宽度均为2m. ,将线段AB的长度l表示为θ的函数;
,将线段AB的长度l表示为θ的函数;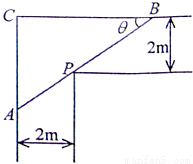 某直角走廊的示意图如图所示,其两边走廊的宽度均为2m.
某直角走廊的示意图如图所示,其两边走廊的宽度均为2m.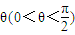 ,将线段AB的长度l表示为θ的函数;
,将线段AB的长度l表示为θ的函数; 某直角走廊的示意图如图所示,其两边走廊的宽度均为2m.
某直角走廊的示意图如图所示,其两边走廊的宽度均为2m.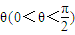 ,将线段AB的长度l表示为θ的函数;
,将线段AB的长度l表示为θ的函数;