题目内容
已知函数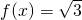 sin(ωx-
sin(ωx- )-cos(ωx-
)-cos(ωx- )(ω>0)图象的两相邻对称轴间的距离为
)(ω>0)图象的两相邻对称轴间的距离为 .
.
(I)求f( )的值;
)的值;
(II)将函数y=f(x)的图象向右平移 个单位后,得到函数y=g(x)图象,求g(x)在区间[0,
个单位后,得到函数y=g(x)图象,求g(x)在区间[0, ]上的单调性.
]上的单调性.
解:(I)函数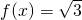 sin(ωx-
sin(ωx- )-cos(ωx-
)-cos(ωx- )
)
=2sin(ωx- -
- )=2sin(ωx-
)=2sin(ωx- )=-2cos(ωx)…(3分)
)=-2cos(ωx)…(3分)
由条件两相邻对称轴间的距离为 .
.
所以T=π, ,所以ω=2,∴f(x)=-2cos2x,f(
,所以ω=2,∴f(x)=-2cos2x,f( )=-
)=- …(6分)
…(6分)
(II)函数y=f(x)的图象向右平移 个单位后,得到函数y=g(x)图象,
个单位后,得到函数y=g(x)图象,
所以g(x)=-2cos(2x- ),
),
令2kπ-π≤2x- ≤2kπ,k∈Z,解得kπ
≤2kπ,k∈Z,解得kπ ≤x≤kπ
≤x≤kπ ,k∈Z
,k∈Z
又x∈[0, ]
]
所以g(x)在[0, ]上递减,在[
]上递减,在[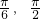 ]上递增…(13分)
]上递增…(13分)
分析:(I)利用两角差的正弦函数以及诱导公式化简函数的表达式,图象的两相邻对称轴间的距离为 ,求出函数的周期,求出ω然后,直接求f(
,求出函数的周期,求出ω然后,直接求f( )的值;
)的值;
(II)将函数y=f(x)的图象向右平移 个单位后,得到函数y=g(x)图象,求出函数的解析式.然后求出函数的单调区间,即可求g(x)在区间[0,
个单位后,得到函数y=g(x)图象,求出函数的解析式.然后求出函数的单调区间,即可求g(x)在区间[0, ]上的单调性.
]上的单调性.
点评:本题是中档题,考查三角函数的化简求值,函数图象的平移,函数的单调性的应用,考查计算能力.
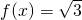 sin(ωx-
sin(ωx- )-cos(ωx-
)-cos(ωx- )
)=2sin(ωx-
 -
- )=2sin(ωx-
)=2sin(ωx- )=-2cos(ωx)…(3分)
)=-2cos(ωx)…(3分)由条件两相邻对称轴间的距离为
 .
.所以T=π,
 ,所以ω=2,∴f(x)=-2cos2x,f(
,所以ω=2,∴f(x)=-2cos2x,f( )=-
)=- …(6分)
…(6分)(II)函数y=f(x)的图象向右平移
 个单位后,得到函数y=g(x)图象,
个单位后,得到函数y=g(x)图象,所以g(x)=-2cos(2x-
 ),
),令2kπ-π≤2x-
 ≤2kπ,k∈Z,解得kπ
≤2kπ,k∈Z,解得kπ ≤x≤kπ
≤x≤kπ ,k∈Z
,k∈Z又x∈[0,
 ]
]所以g(x)在[0,
 ]上递减,在[
]上递减,在[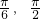 ]上递增…(13分)
]上递增…(13分)分析:(I)利用两角差的正弦函数以及诱导公式化简函数的表达式,图象的两相邻对称轴间的距离为
 ,求出函数的周期,求出ω然后,直接求f(
,求出函数的周期,求出ω然后,直接求f( )的值;
)的值;(II)将函数y=f(x)的图象向右平移
 个单位后,得到函数y=g(x)图象,求出函数的解析式.然后求出函数的单调区间,即可求g(x)在区间[0,
个单位后,得到函数y=g(x)图象,求出函数的解析式.然后求出函数的单调区间,即可求g(x)在区间[0, ]上的单调性.
]上的单调性.点评:本题是中档题,考查三角函数的化简求值,函数图象的平移,函数的单调性的应用,考查计算能力.

练习册系列答案
相关题目
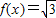 sin(ωx-
sin(ωx- )-cos(ωx-
)-cos(ωx- )(ω>0)图象的两相邻对称轴间的距离为
)(ω>0)图象的两相邻对称轴间的距离为 .
. )的值;
)的值; 个单位后,得到函数y=g(x)图象,求g(x)在区间[0,
个单位后,得到函数y=g(x)图象,求g(x)在区间[0, ]上的单调性.
]上的单调性.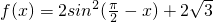 sin(π-x)cosx,
sin(π-x)cosx, 上的值域;
上的值域;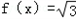 sin(
sin(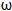 x﹣
x﹣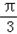 )﹣cos(
)﹣cos(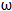 x﹣
x﹣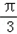 )(
)(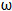 >0)图象的两相邻对称轴间的距离为
>0)图象的两相邻对称轴间的距离为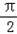 .
. 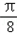 )的值;
)的值;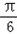 个单位后,得到函数y=g(x)图象,求g(x)在区间[0,
个单位后,得到函数y=g(x)图象,求g(x)在区间[0,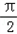 ]上的单调性.
]上的单调性.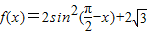 sin(π-x)cosx,
sin(π-x)cosx,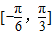 上的值域;
上的值域;