题目内容
(06年湖北卷文)(12分)
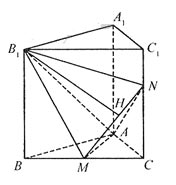
如图,已知正三棱柱ABC-A1B1C1的侧棱长和底面边长均为1,M是底面BC边上的中点,N是侧棱CC1上的点,且CN=2C1N.
(Ⅰ)求二面角B1-AM-N的平面角的余弦值;
(Ⅱ)求点B1到平面AMN的距离。

解析:解法1:(Ⅰ)因为M是底面BC边上的中点,所以AM![]() BC,又AM
BC,又AM![]() C
C![]() ,所以AM
,所以AM![]() 面BC
面BC![]()
![]() ,从而AM
,从而AM![]()
![]() M, AM
M, AM![]() NM,所以
NM,所以![]()
![]() MN为二面角,
MN为二面角,![]() ―AM―N的平面角。又
―AM―N的平面角。又![]() M=
M=![]()
![]() ,MN=
,MN=![]() ,
,
连![]() N,得
N,得![]() N=
N=![]() ,在
,在![]()
![]() MN中,由余弦定理得
MN中,由余弦定理得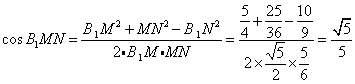 。故所求二面角
。故所求二面角![]() ―AM―N的平面角的余弦值为
―AM―N的平面角的余弦值为![]() 。
。
(Ⅱ)过![]() 在面
在面![]() 内作直线
内作直线![]() ,
,![]() 为垂足。又
为垂足。又![]() 平面
平面![]() ,所以AM
,所以AM![]()
![]() H。于是
H。于是![]() H
H![]() 平面AMN,故
平面AMN,故![]() H即为
H即为![]() 到平面AMN的距离。在
到平面AMN的距离。在![]() 中,
中,![]() H=
H=![]() M
M![]() 。故点
。故点![]() 到平面AMN的距离为1。
到平面AMN的距离为1。
解法2:(Ⅰ)建立如图所示的空间直角坐标系,
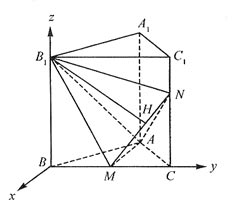
则![]() (0,0,1),M(0,
(0,0,1),M(0,![]() ,0),
,0),
C(0,1,0), N (0,1,![]() ) , A (
) , A (![]() ),所以,
),所以,
![]() ,
,![]() ,
,![]() 。
。
因为
![]() 所以
所以![]() ,同法可得
,同法可得![]() 。
。
故![]() 为二面角
为二面角![]() ―AM―N的平面角
―AM―N的平面角
∴![]()
![]() =
=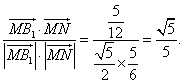
故所求二面角![]() ―AM―N的平面角的余弦值为
―AM―N的平面角的余弦值为![]() 。
。
(Ⅱ)设n=(x,y,z)为平面AMN的一个法向量,则由![]() 得
得
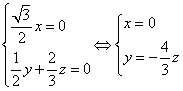 故可取
故可取![]()
设![]() 与n的夹角为a,则
与n的夹角为a,则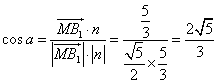 。
。
所以![]() 到平面AMN的距离为
到平面AMN的距离为![]() 。
。

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
