题目内容
矩阵
可逆的一个充分不必要条件是（ ）A．ad-bc≠0
B．ab-cd≠0
C．
D．
【答案】分析：根据矩阵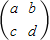
可逆的充要条件是所对应的行列式|A|≠0即ab-cd≠0，再根据充分不必要条件的性质可得结论．
解答：解：∵
∴ab-cd≠0即|A|≠0，则矩阵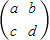
可逆
当矩阵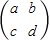
可逆，则|A|≠0即ab-cd≠0，但
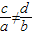不一定成立
所以
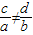是矩阵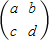
可逆的一个充分不必要条件
故选C．
点评：本题主要考查了矩阵存在逆矩阵的充要条件，同时考查了必要条件、充分条件与充要条件的判断，属于基础题．
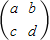可逆的充要条件是所对应的行列式|A|≠0即ab-cd≠0，再根据充分不必要条件的性质可得结论．解答：解：∵
∴ab-cd≠0即|A|≠0，则矩阵
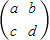可逆当矩阵
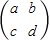可逆，则|A|≠0即ab-cd≠0，但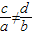不一定成立所以
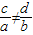是矩阵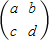可逆的一个充分不必要条件故选C．
点评：本题主要考查了矩阵存在逆矩阵的充要条件，同时考查了必要条件、充分条件与充要条件的判断，属于基础题．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
矩阵
可逆的一个充分不必要条件是（ ）
|
| A、ad-bc≠0 | ||||
| B、ab-cd≠0 | ||||
C、
| ||||
D、
|