题目内容
设A1、A2是椭圆
+
=1(a>b>0)长轴的两个端点,P1P2是垂直于x轴的弦,求直线A1P1、A2P2的交点P的轨迹方程.
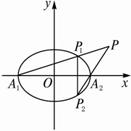
解析:设A1(-a,0),A2(a,0),P1(x0,y0),P2(x0,-y0),
则l A1P1:y=(x+a),l A2P2:y=
(x-a).
两式相乘得y2=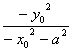
(x2-a2),注意到
+
=1,
∴直线A1P1、A2P2交点P的轨迹方程是
-
=1(y≠0).
练习册系列答案
相关题目
设A1、A2是椭圆
+
=1=1的长轴两个端点，P1、P2是垂直于A1A2的弦的端点，则直线A1P1与A2P2交点的轨迹方程为（ ）
| x2 |
| 9 |
| y2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
=1的长轴两个端点，P1、P2是垂直于A1A2的弦的端点，则直线A1P1与A2P2交点P的轨迹方程为( )
=1 B.
=1
=1 D.
=1
+
=1的长轴的两个端点，P1、P2是垂直于A1A2的弦的端点，则直线A1P1与A2P2交点的轨迹方程为
+
=1 B.
+
=1
=1 D.
=1
=1的长轴两个端点，P1、P2是垂直于A1A2的弦的端点，则直线A1P1与A2P2交点的轨迹方程为( )
B
D