题目内容
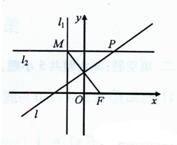 已知点F(1,0)和直线l1:x=-1,直线l2过直线l1上的动点M且与直线l1垂直,线段MF的垂直平分线l与直线l2相交于点P.
已知点F(1,0)和直线l1:x=-1,直线l2过直线l1上的动点M且与直线l1垂直,线段MF的垂直平分线l与直线l2相交于点P.(I)求点P的轨迹C的方程;
(II)设直线PF与轨迹C相交于另一点Q,与直线l1相交于点N,求
| NP |
| NQ |
分析:(I)由题意可得,点P到点F(1,0)的距离等于点P到直线l1:x=-1的距离,由抛物线的定义可得点P的轨迹是抛物线,从而求得方程.
(II)把直线PF的方程y=k(x-1)代入y2=4x化简,把根与系数的关系代入
•
=|
•|
|=
|x1+1|•
|x2+1| 化简,再利用基本不等式求得
•
的最小值.
(II)把直线PF的方程y=k(x-1)代入y2=4x化简,把根与系数的关系代入
| NP |
| NQ |
| NP| |
| NQ |
| 1+k2 |
| 1+k2 |
| NP |
| NQ |
解答:解:(I)连接PF,∵MF的中垂线l交l2于点P,∴|PF|=|PM|,即点P到点F(1,0)的距离等于
点P到直线l1:x=-1的距离,由抛物线的定义可得点P的轨迹C是以F为焦点,以直线l1:x=-1为准线的抛物线,
方程为 y2=4x.
(II)把直线PF的方程y=k(x-1)代入y2=4x可得 k2x2-(2k2+4)x+k2=0,k≠0,且△>0.
且x1+x2=
,x1•x2=1.∵
和
同向,N(-1,-2k),
∴
•
=|
•|
|=
|x1+1|•
|x2+1|=(1+k2)(x1•x2+x1+x2+1 )
=4(k2+
+2)≥16,当且仅当k=±1时,等号成立.
∴
•
的最小值为16.
点P到直线l1:x=-1的距离,由抛物线的定义可得点P的轨迹C是以F为焦点,以直线l1:x=-1为准线的抛物线,
方程为 y2=4x.
(II)把直线PF的方程y=k(x-1)代入y2=4x可得 k2x2-(2k2+4)x+k2=0,k≠0,且△>0.
且x1+x2=
| 2k2+4 |
| k2 |
| NP |
| NQ |
∴
| NP |
| NQ |
| NP| |
| NQ |
| 1+k2 |
| 1+k2 |
=4(k2+
| 1 |
| k2 |
∴
| NP |
| NQ |
点评:本题考查抛物线的定义,一元二次方程根与系数的关系,基本不等式的应用,得到
•
=|
•|
|=
|x1+1|•
|x2+1| 是解题的关键.
| NP |
| NQ |
| NP| |
| NQ |
| 1+k2 |
| 1+k2 |

练习册系列答案
相关题目
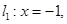 直线
直线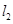 过直线
过直线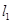 上的动点M且与直线
上的动点M且与直线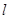 与直线
与直线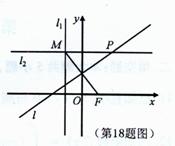
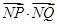 的最小值
的最小值