题目内容
(08年重庆卷理)(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分.)
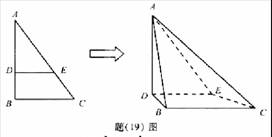
如题(19)图,在![]() 中,B=
中,B=![]() ,AC=
,AC=![]() ,D、E两点分别在AB、AC上.使
,D、E两点分别在AB、AC上.使
![]() ,DE=3.现将
,DE=3.现将![]() 沿DE折成直二角角,求:
沿DE折成直二角角,求:
(Ⅰ)异面直线AD与BC的距离;
(Ⅱ)二面角A-EC-B的大小(用反三角函数表示).
【标准答案】 解法一:
(Ⅰ)在答(19)图1中,因![]() ,故BE∥BC.又因B=90°,从而
,故BE∥BC.又因B=90°,从而
AD⊥DE.
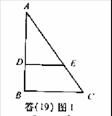
在第(19)图2中,因A-DE-B是直二面角,AD⊥DE,故AD⊥底面DBCE,从
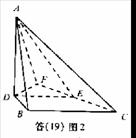
而AD⊥DB.而DB⊥BC,故DB为异面直线AD与BC的公垂线.
下求DB之长.在答(19)图1中,由![]() ,得
,得![]()
又已知DE=3,从而![]()
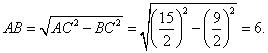
因![]()
(Ⅱ)在第(19)图2中,过D作DF⊥CE,交CE的延长线于F,连接AF.由(1)知,
AD⊥底面DBCE,由三垂线定理知AF⊥FC,故∠AFD为二面角A-BC-B的平面
角.
在底面DBCE中,∠DEF=∠BCE,
![]()
因此![]()
从而在Rt△DFE中,DE=3,
![]()
在![]()
因此所求二面角A-EC-B的大小为arctan![]()
解法二:
(Ⅰ)同解法一.
(Ⅱ)如答(19)图3.由(Ⅰ)知,

以D点为坐标原点,![]() 的方向为x、
的方向为x、
y、z轴的正方向建立空间直角坐标系,则D(0,0,0),A(0,0,4),
![]() ,E(0,3,0).
,E(0,3,0).
![]() 过D作DF⊥CE,交CE的延长线于F,连接AF.
过D作DF⊥CE,交CE的延长线于F,连接AF.
设![]() 从而
从而![]()
![]() ,有
,有
![]() ①
①
又由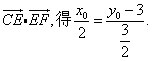 ②
②
联立①、②,解得![]()
因为![]() ,故
,故![]() ,又因
,又因![]() ,所以
,所以![]() 为所求的二面角A-EC-B的平面角.因
为所求的二面角A-EC-B的平面角.因![]() 有
有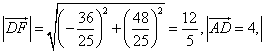 所以
所以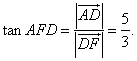
因此所求二面角A-EC-B的大小为![]()
【高考考点】本题主要考查直线、直线与平面、平面与平面的位置关系、异面直线间的距离等知识,考查空间想象能力和思维能力,利用综合法或向量法解决立体几何问题的能力。
【易错提醒】
【备考提示】立体几何中的平行、垂直、二面角是考试的重点。

