题目内容
设sinα=sinθ+cosθ，sin2β=2sinθ•cosθ，则（ ）
| A．sin2α=1+sin2β | B．sin2α=1+2sin2β |
| C．sin2α=1-sin2β | D．sin2α=1-2sin2β |
∵sinα=sinθ+cosθ，sin2β=2sinθ•cosθ
∴sin2α=sin2θ+cos2θ+2sinθ•cosθ，
∴sin2α=1+sin2β，
故选A．
∴sin2α=sin2θ+cos2θ+2sinθ•cosθ，
∴sin2α=1+sin2β，
故选A．
练习册系列答案
阅读快车系列答案
相关题目
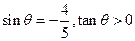，则
.
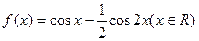的最大值等于 ．
( )
，则
等于（ ）
