题目内容
设实数a>1,若仅有一个常数c使得对于任意的x∈[a,3a],都有y∈[a,a2]满足方程logax+logay=c,这时,实数a的取值的集合为 .
【答案】分析:由题意可得x>0,y>0,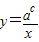 ,作出其图象如图所示,进而得出
,作出其图象如图所示,进而得出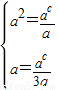 及a>1,c只有一个值.解出即可.
及a>1,c只有一个值.解出即可.
解答:解:∵logax+logay=c,∴x>0,y>0,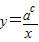 .(a>1),作出其函数图象:
.(a>1),作出其函数图象: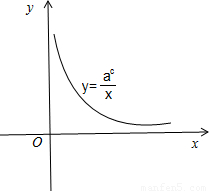
由图象可以看出:函数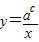 在区间[a,3a]上单调递减,
在区间[a,3a]上单调递减,
∴必有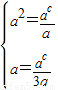 及a>1,c只有一个值.解得c=3,a=3.适合题意.
及a>1,c只有一个值.解得c=3,a=3.适合题意.
∴实数a的取值的集合为{3}.
点评:由题意确定函数的单调性和画出其图象是解题的关键.
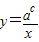 ,作出其图象如图所示,进而得出
,作出其图象如图所示,进而得出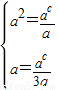 及a>1,c只有一个值.解出即可.
及a>1,c只有一个值.解出即可.解答:解:∵logax+logay=c,∴x>0,y>0,
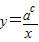 .(a>1),作出其函数图象:
.(a>1),作出其函数图象: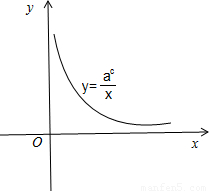
由图象可以看出:函数
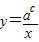 在区间[a,3a]上单调递减,
在区间[a,3a]上单调递减,∴必有
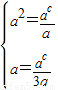 及a>1,c只有一个值.解得c=3,a=3.适合题意.
及a>1,c只有一个值.解得c=3,a=3.适合题意.∴实数a的取值的集合为{3}.
点评:由题意确定函数的单调性和画出其图象是解题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目