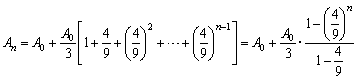题目内容
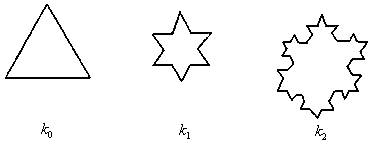
有一个雪花曲线序列,其产生的规则是:将正三角形k0的每一边三等分,而以其居中的那一线段为底边向外作等边三角形,再擦去中间的那条边,便得第一条雪花曲线k1,再将k1的每一边三等分,并重复上述作法,便得第二条雪花曲线k2…把kn-1的每一边三等分,并以中间那条线段向外作等边三角形, 再擦去中间的那条边, 便得第n条雪花曲线kn(n=2,3,4,…)。
(1) 设k0的周长为L0,即正三角形的周长,求kn,即第n条雪花曲线的周长Ln;
(2) 设k0的面积为A0,即正三角形的面积,求kn即第n条雪花曲线围成的面积An;
(3)随着n的增大,Ln和An的极限是否存在?
答案:
解析:
解析:
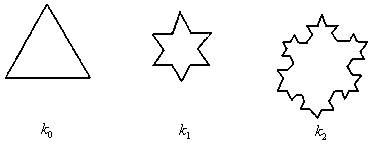
解:(1)在雪花曲线序列中,将kn-1变为kn,后一曲线的同等是前一曲线同等的 (2)k0,k1,k2,…,kn,…的边数依次为3,3×4,3×42,…,3×4n,…,因此,k1比k0多出了3个面积为
由
(3)由
|

练习册系列答案
相关题目