题目内容
已知平面区域D1={（x，y）|
|
| 1 |
| 8 |
分析：本题考查的知识点是几何概型的意义，关键是要找出D1、D2对应面积的大小，然后将其代入几何概型的计算公式进行求解．在解题过程中，注意三角形面积的应用．
解答：
解：依题意可在平面直角坐标系中作出集合D1所表示的平面区域是正方形与D2所表示的平面区域是阴影部分的三角形（如图），
由图可知D1=16，
由于0＜p≤
则
0＜D2≤2．由于直线恒过点（0，2），
则kx-y+2＜0的斜率k的取值范围是：[-1，0）∪（0，1]．
故答案为：[-1，0）∪（0，1]．
解：依题意可在平面直角坐标系中作出集合D1所表示的平面区域是正方形与D2所表示的平面区域是阴影部分的三角形（如图），由图可知D1=16，
由于0＜p≤
| 1 |
| 8 |
0＜D2≤2．由于直线恒过点（0，2），
则kx-y+2＜0的斜率k的取值范围是：[-1，0）∪（0，1]．
故答案为：[-1，0）∪（0，1]．
点评：本题考查的知识点是二元一次不等式（组）与平面区域、几何概型的意义，关键是要找出D对应面积的大小，并将其面积代入几何概型计算公式进行求解．几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．
练习册系列答案
相关题目
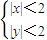}，D2={（x，y）|kx-y+2＜0}．在区域D1内随机选取一点若点M恰好取自区域D2的概率为p，且0＜p≤
则A的取值范围是 ．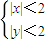
}，D2={（x，y）|kx-y+2＜0}．在区域D1内随机选取一点若点M恰好取自区域D2的概率为p，且0＜p≤
则A的取值范围是 ．
|
，，D2={（x，y）|（x-2）2+（y-2）2＜4}．在区域D1内随机选取一点P，则点P恰好取自区域D2的概率是（ ）
