题目内容
(06年天津卷理)(14分)
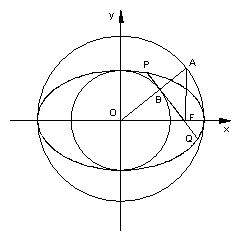
如图,以椭圆![]() 的中心O为圆心,分别以
的中心O为圆心,分别以![]() 和
和![]() 为半径作大圆和小圆。过椭圆右焦点
为半径作大圆和小圆。过椭圆右焦点![]() 作垂直于
作垂直于![]() 轴的直线交大圆于第一象限内的点A。连结OA交小圆于点B。设直线BF是小圆的切线。
轴的直线交大圆于第一象限内的点A。连结OA交小圆于点B。设直线BF是小圆的切线。
(I)证明![]() 并求直线BF与
并求直线BF与![]() 同的交点M的坐标;
同的交点M的坐标;
(II)设直线BF交椭圆P、Q两点,证明![]()
解析:(I)证明:由题设条件知,![]() 故
故
![]() 即
即![]()
因此,![]() ①
①
在![]() 中,
中,![]()
于是,直线OA的斜率![]() 设直线BF的斜率为
设直线BF的斜率为![]() 则
则
![]()
这时,直线BF的方程为![]() 令
令![]() 则
则![]()
所以直线BF与![]() 轴的交点为
轴的交点为![]()

(II)证明:由(I),得直线![]() 的方程为
的方程为![]() 且
且
![]() ②
②
由已知,设![]() 、
、![]() 则它们的坐标满足方程组
则它们的坐标满足方程组
 ③
③
由方程组③消去![]() 并整理得
并整理得
![]() ④
④
由式①、②和④,

由方程组③消去![]() 并整理得
并整理得
![]() ⑤
⑤
由式②和⑤,

综上,得到
![]()
注意到![]() 得
得
![]()

【高考考点】椭圆的标准方程和几何性质 直线方程 平面向量 曲线和方程的关系
【易错点】:不能找出隐含条件![]() 结合
结合![]() 完成第一问证明,第二问到
完成第一问证明,第二问到![]() 的计算及
的计算及![]() 向结论的化简过程
向结论的化简过程
【备考提示】:掌握椭圆的几何性质,善于找出已知中的隐含条件是解决此题的关键

练习册系列答案
相关题目