题目内容
(本题满分50分)设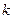 ,
,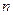 为给定的整数,
为给定的整数,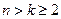 . 对任意
. 对任意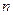 元的数集
元的数集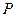 ,作
,作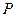 的所有
的所有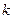 元子集的元素和,记这些和组成的集合为
元子集的元素和,记这些和组成的集合为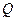 ,集合
,集合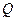 中元素个数是
中元素个数是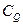 ,求
,求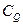 的最大值.
的最大值.
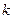 ,
,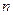 为给定的整数,
为给定的整数,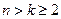 . 对任意
. 对任意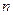 元的数集
元的数集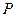 ,作
,作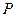 的所有
的所有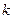 元子集的元素和,记这些和组成的集合为
元子集的元素和,记这些和组成的集合为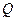 ,集合
,集合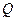 中元素个数是
中元素个数是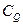 ,求
,求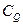 的最大值.
的最大值. 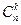
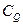 的最大值为
的最大值为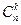 . ……10分因
. ……10分因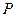 共有
共有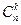 个
个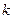 元子集,故显然有
元子集,故显然有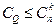 .…20分
.…20分下面我们指出,对集合
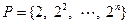 ,相应的
,相应的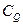 等于
等于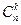 ,即
,即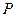 的任意两个不同的
的任意两个不同的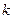
元子集的元素之和不相等. 从而
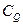 的最大值为
的最大值为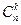 .事实上,若上述的集合
.事实上,若上述的集合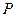 有两个不同的
有两个不同的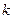 元子集
元子集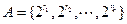 ,
, 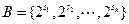 ,使得
,使得 与
与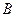 的元素之和相等,则
的元素之和相等,则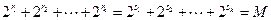 (设). ①因①可视为正整数
(设). ①因①可视为正整数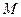 的二进制表示,由于
的二进制表示,由于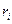 互不相同,
互不相同,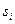 互不相同,故由正整数的二进制表示的唯一性,我们由①推出,集合
互不相同,故由正整数的二进制表示的唯一性,我们由①推出,集合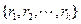 必须与
必须与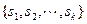 相同,从而子集
相同,从而子集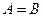 ,矛盾.这就证明了我们的断言. 50分
,矛盾.这就证明了我们的断言. 50分
练习册系列答案
相关题目
 双鞋中任取
双鞋中任取 只,其中恰好有
只,其中恰好有 双的取法种数为( )
双的取法种数为( )



 的九个数字里,任取四个数字排成一个首末两个数字是奇数的四位数,这样的四位数有_________________个?
的九个数字里,任取四个数字排成一个首末两个数字是奇数的四位数,这样的四位数有_________________个?
 的最小值,使得存在以红点为顶点的
的最小值,使得存在以红点为顶点的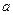 个,四位偶数有
个,四位偶数有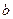 个,求
个,求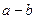 的值;
的值; ,求
,求 .
.