题目内容
给出下列结论.
①命题“?x∈R,cosx>0”的否定是“?x∈R,cosx≤0”;
②将函数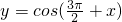 的图象上每个点的横坐标缩短为原来的
的图象上每个点的横坐标缩短为原来的 (纵坐标不变),再向左平行移动
(纵坐标不变),再向左平行移动 个单位长度变为函数
个单位长度变为函数 的图象;
的图象;
③已知ξ~N(16,σ2),若P(ξ>17)=0.35,则P(15<ξ<16)=0.15;
④已知函数f(x)=|lgx|,若0<a<b,且f(a)=f(b),则a+2b的取值范围是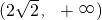 ;
;
其中真命题的序号是________(把所有真命题的序号都填上).
①③
分析:①直接把语句进行否定即可,注意否定时?对应?,>对应≤.
②先进行ω伸缩变换,再根据左加右减的性质先左右平移即可得到答案.
③根据随机变量ξ服从标准正态分布N(16,σ2),得到正态曲线关于ξ=16对称,得到变量小于15的概率,这样要求的概率是用0.5减去P(ξ>17)的值即得.
④画出函数f(x)的图象,则数形结合可知0<a<1,b>1,且ab=1,再将所求a+2b化为关于a的一元函数,利用函数单调性求函数的值域即可.
解答:①根据题意我们直接对语句进行否定,
命题“?x∈R,cosx>0”的否定是“?x∈R,cosx≤0”;正确.
②:由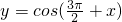 =sinx的图象上每个点的横坐标缩短为原来的
=sinx的图象上每个点的横坐标缩短为原来的 (纵坐标不变),得到y=sin2x,
(纵坐标不变),得到y=sin2x,
再向左平行移动 个单位长度变为函数y=sin2(x+
个单位长度变为函数y=sin2(x+ )=sin(2x+
)=sin(2x+ ).
).
故不正确.
③:∵随机变量ξ服从标准正态分布N(16,σ2),
∴正态曲线关于ξ=16对称,
∵P(ξ>17)=0.35
若P(ξ<15)=0.35,
则P(15<ξ<16)=0.5-0.35=0.15,正确;
 ④:画出y=|lgx|的图象如图:
④:画出y=|lgx|的图象如图:
∵0<a<b,且f(a)=f(b),
∴|lga|=|lgb|且0<a<1,b>1
∴-lga=lgb
即ab=1
∴y=a+2b=a+ ,a∈(0,1)
,a∈(0,1)
∵y=a+ 在(0,1)上为减函数,
在(0,1)上为减函数,
∴y>1+2=3
∴a+2b的取值范围是(3,+∞),故不正确.
故答案为:①③
点评:本题考查函数的变换,函数的单调性,特称命题,正态分布曲线的特点及曲线所表示的意义,考查学生分析问题解决问题的能力,是基础题.
分析:①直接把语句进行否定即可,注意否定时?对应?,>对应≤.
②先进行ω伸缩变换,再根据左加右减的性质先左右平移即可得到答案.
③根据随机变量ξ服从标准正态分布N(16,σ2),得到正态曲线关于ξ=16对称,得到变量小于15的概率,这样要求的概率是用0.5减去P(ξ>17)的值即得.
④画出函数f(x)的图象,则数形结合可知0<a<1,b>1,且ab=1,再将所求a+2b化为关于a的一元函数,利用函数单调性求函数的值域即可.
解答:①根据题意我们直接对语句进行否定,
命题“?x∈R,cosx>0”的否定是“?x∈R,cosx≤0”;正确.
②:由
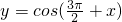 =sinx的图象上每个点的横坐标缩短为原来的
=sinx的图象上每个点的横坐标缩短为原来的 (纵坐标不变),得到y=sin2x,
(纵坐标不变),得到y=sin2x,再向左平行移动
 个单位长度变为函数y=sin2(x+
个单位长度变为函数y=sin2(x+ )=sin(2x+
)=sin(2x+ ).
).故不正确.
③:∵随机变量ξ服从标准正态分布N(16,σ2),
∴正态曲线关于ξ=16对称,
∵P(ξ>17)=0.35
若P(ξ<15)=0.35,
则P(15<ξ<16)=0.5-0.35=0.15,正确;
 ④:画出y=|lgx|的图象如图:
④:画出y=|lgx|的图象如图:∵0<a<b,且f(a)=f(b),
∴|lga|=|lgb|且0<a<1,b>1
∴-lga=lgb
即ab=1
∴y=a+2b=a+
 ,a∈(0,1)
,a∈(0,1)∵y=a+
 在(0,1)上为减函数,
在(0,1)上为减函数,∴y>1+2=3
∴a+2b的取值范围是(3,+∞),故不正确.
故答案为:①③
点评:本题考查函数的变换,函数的单调性,特称命题,正态分布曲线的特点及曲线所表示的意义,考查学生分析问题解决问题的能力,是基础题.

练习册系列答案
相关题目