题目内容
选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线C的参数方程为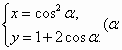 为参数),点M的坐标为(-1,1);若以该直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,
为参数),点M的坐标为(-1,1);若以该直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,
(1)请将点M的直角坐标化为极坐标(限定ρ≥0,-π<![]() ≤π);
≤π);
(2)求出以M为圆心,半径为![]() 的圆的极坐标方程.
的圆的极坐标方程.
(3)若点N是曲线C上的任一点,求线段MN的长度的最大值和最小值.
答案:
解析:
解析:
|
解:(1) 即点M的极坐标 (2)所求的圆的极坐标方程是 (3) 故当 |

练习册系列答案
相关题目
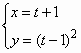 (t为参数);相交于A,B两点,则线段AB的中点的直角坐标为________.
(t为参数);相交于A,B两点,则线段AB的中点的直角坐标为________.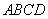 是边长为
是边长为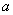 的正方形,以
的正方形,以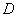 为圆心,
为圆心,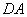 为半径的圆弧与以
为半径的圆弧与以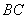 为直径的
为直径的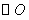 交于点
交于点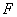 ,延长
,延长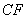 交
交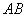 于
于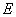 .(1)求证:
.(1)求证: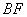 的长.
的长.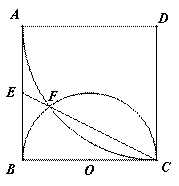
 ,若矩阵
,若矩阵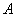 属于特征值3的一个特征向量为
属于特征值3的一个特征向量为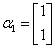 ,属于特征值-1的一个特征向量为
,属于特征值-1的一个特征向量为 ,求矩阵
,求矩阵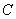 的极坐标方程为
的极坐标方程为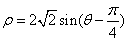 ,以极点为原点,极轴为
,以极点为原点,极轴为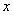 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线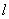 的参数方程为
的参数方程为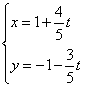 (
(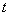 为参数),求直线
为参数),求直线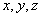 满足
满足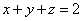 ,求
,求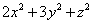 的最小值;
的最小值;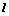 经过点P(1,1),倾斜角
经过点P(1,1),倾斜角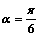 ,
,