题目内容
如图所示,质点P在正方形ABCD的四个顶点上按逆时针方向前进.现在投掷一个质地均匀、每个面上标有一个数字的正方体玩具,它的六个面上分别写有两个1、两个2、两个3一共六个数字.质点P从A点出发,规则如下:当正方体上底面出现的数字是1,质点P前进一步(如由A到B);当正方体上底面出现的数字是2,质点P前进两步(如由A到C),当正方体上底面出现的数字是3,质点P前进三步(如由A到D).在质点P转一圈之前连续投掷,若超过一圈,则投掷终止.
(1)求质点P恰好返回到A点的概率;
(2)在质点P转一圈恰能返回到A点的所有结果中,用随机变量ξ表示点P恰能返回到A点的投掷次数,求ξ的数学期望.
(1)求质点P恰好返回到A点的概率;
(2)在质点P转一圈恰能返回到A点的所有结果中,用随机变量ξ表示点P恰能返回到A点的投掷次数,求ξ的数学期望.

(1) P=P2+P3+P4= +
+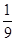 +
+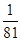 =
=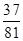 .
.
(2) Eξ=2×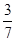 +3×
+3×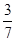 +4×
+4×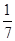 =
=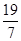 .
.
 +
+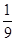 +
+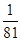 =
=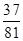 .
. (2) Eξ=2×
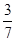 +3×
+3×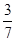 +4×
+4×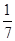 =
=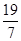 .
. (1)由古典概型概率公式得投掷一次正方体玩具,每个数字在上底面的概率为P1=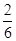 =
= .再分析质点P恰好返回到A点共有三种情况,投掷两次质点P返回到A点,有(1,3)、(3,1)、(2,2)三种结果;投掷三次质点P返回到A点,有 (1,1,2)、(1,2,1)、(2,1,1)三种结果;投掷四次质点P返回到A点,只有 (1,1,1,1).根据相互独立事件和互斥事件的概率公式求解;
.再分析质点P恰好返回到A点共有三种情况,投掷两次质点P返回到A点,有(1,3)、(3,1)、(2,2)三种结果;投掷三次质点P返回到A点,有 (1,1,2)、(1,2,1)、(2,1,1)三种结果;投掷四次质点P返回到A点,只有 (1,1,1,1).根据相互独立事件和互斥事件的概率公式求解;
(2)由(1)得随机变量ξ的值为2,3,4,分别求出对应的概率,根据期望公式计算得Eξ
(1)投掷一次正方体玩具,每个数字在上底面出现都是等可能的,其概率为P1=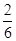 =
= .
.
只投掷一次不可能返回到A点;若投掷两次质点P就恰好能返回到A点,则上底面出现的两个数字应依次为:(1,3)、(3,1)、(2,2)三种结果,其概率为P2=( )2×3=
)2×3= ;
;
若投掷三次质点P恰能返回到A点,则上底面出现的三个数字应依次为:(1,1,2)、(1,2,1)、(2,1,1)三种结果,其概率为P3=( )3×3=
)3×3=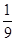 ;
;
若投掷四次质点P恰能返回到A点,则上底面出现的四个数字应依次为:(1,1,1,1).其概率为P4=( )4=
)4=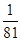 .
.
所以,质点P恰好返回到A点的概率为:P=P2+P3+P4= +
+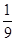 +
+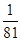 =
=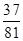 . 6分
. 6分
(2)由(1)知,质点P转一圈恰能返回到A点的所有结果共有以上问题中的7种情况,且ξ的可能取值为2,3,4,
则P(ξ=2)=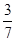 ,P(ξ=3)=
,P(ξ=3)=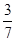 ,P(ξ=4)=
,P(ξ=4)=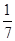 ,
,
所以,Eξ=2×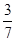 +3×
+3×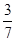 +4×
+4×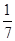 =
=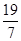 .
.
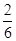 =
= .再分析质点P恰好返回到A点共有三种情况,投掷两次质点P返回到A点,有(1,3)、(3,1)、(2,2)三种结果;投掷三次质点P返回到A点,有 (1,1,2)、(1,2,1)、(2,1,1)三种结果;投掷四次质点P返回到A点,只有 (1,1,1,1).根据相互独立事件和互斥事件的概率公式求解;
.再分析质点P恰好返回到A点共有三种情况,投掷两次质点P返回到A点,有(1,3)、(3,1)、(2,2)三种结果;投掷三次质点P返回到A点,有 (1,1,2)、(1,2,1)、(2,1,1)三种结果;投掷四次质点P返回到A点,只有 (1,1,1,1).根据相互独立事件和互斥事件的概率公式求解;(2)由(1)得随机变量ξ的值为2,3,4,分别求出对应的概率,根据期望公式计算得Eξ
(1)投掷一次正方体玩具,每个数字在上底面出现都是等可能的,其概率为P1=
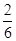 =
= .
.只投掷一次不可能返回到A点;若投掷两次质点P就恰好能返回到A点,则上底面出现的两个数字应依次为:(1,3)、(3,1)、(2,2)三种结果,其概率为P2=(
 )2×3=
)2×3= ;
;若投掷三次质点P恰能返回到A点,则上底面出现的三个数字应依次为:(1,1,2)、(1,2,1)、(2,1,1)三种结果,其概率为P3=(
 )3×3=
)3×3=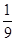 ;
;若投掷四次质点P恰能返回到A点,则上底面出现的四个数字应依次为:(1,1,1,1).其概率为P4=(
 )4=
)4=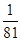 .
.所以,质点P恰好返回到A点的概率为:P=P2+P3+P4=
 +
+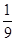 +
+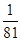 =
=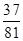 . 6分
. 6分(2)由(1)知,质点P转一圈恰能返回到A点的所有结果共有以上问题中的7种情况,且ξ的可能取值为2,3,4,
则P(ξ=2)=
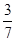 ,P(ξ=3)=
,P(ξ=3)=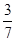 ,P(ξ=4)=
,P(ξ=4)=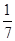 ,
,所以,Eξ=2×
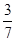 +3×
+3×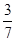 +4×
+4×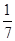 =
=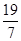 .
.
练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 )=
)= ,则P(Y
,则P(Y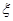 ,求随机变量
,求随机变量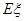 .(8分)
.(8分)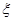 .
. ,一等品率提高为
,一等品率提高为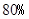 .如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?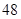 名同学,一次考试后的数学成绩服从正态分布
名同学,一次考试后的数学成绩服从正态分布 ,则理论上
,则理论上 分到
分到  分的人数是 ( )
分的人数是 ( ) 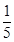
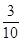




 ),则
),则 (X=2)= ▲ .(用分数表示)
(X=2)= ▲ .(用分数表示)