题目内容
已知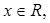 符号
符号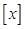 表示不超过
表示不超过 的最大整数,若函数
的最大整数,若函数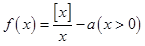 有且仅有3个零点,则
有且仅有3个零点,则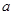 的取值范围是( )
的取值范围是( )
A. | B.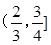 | C.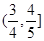 | D. |
C
解析试题分析:因为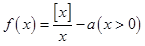 ,有且仅有3个零点,则方程
,有且仅有3个零点,则方程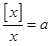 在(0,+∞)上有且仅有3个实数根,且 a>0.∵x>0,∴[x]≥0; 若[x]=0,则
在(0,+∞)上有且仅有3个实数根,且 a>0.∵x>0,∴[x]≥0; 若[x]=0,则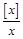 =0;
=0;
若[x]≥1,因为[x]≤x<[x]+1,∴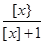 <
<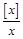 <1,
<1,
∴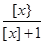 <a≤1,且
<a≤1,且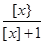 随着[x]的增大而增大.故不同的[x]对应不同的a值,故有[x]=1,2,3,4.
随着[x]的增大而增大.故不同的[x]对应不同的a值,故有[x]=1,2,3,4.
若[x]=1,则有  <
<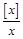 ≤1;
≤1;
若[x]=2,则有  <
<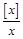 ≤1;
≤1;
若[x]=3,则有  <
<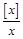 ≤1;
≤1;
若[x]=4,则有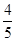 <
<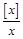 ≤1;
≤1;
综上所述,  <a≤
<a≤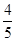 ,故选C.
,故选C.
考点:函数零点,对新概念的理解,分类整合思想

练习册系列答案
相关题目
已知函数 是周期为2的周期函数,且当
是周期为2的周期函数,且当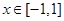 时,
时,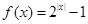 ,则函数
,则函数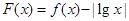 的零点个数是( )
的零点个数是( )
| A.9 | B.10 | C.11 | D.12 |
下列函数中,既是奇函数又是增函数的为( )
A.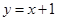 | B.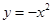 | C.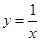 | D.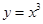 |
已知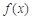 是定义在
是定义在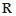 上的奇函数,当
上的奇函数,当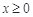 时,
时,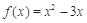 .则函数
.则函数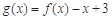
的零点的集合为
A.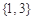 | B.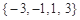 |
C.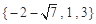 | D.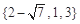 |
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( ).
| A.y=cos2x,x∈R | B.y=log2|x|,x∈R且x≠0) |
C.y=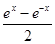 ,x∈R ,x∈R | D.y=x3+1,x∈R |
下列函数中与函数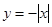 奇偶性相同且在(-∞,0)上单调性也相同的是( ).
奇偶性相同且在(-∞,0)上单调性也相同的是( ).
A.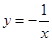 | B. | C.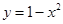 | D.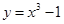 |
已知函数y=f(x)的周期为2,当x∈[-1,1]时f(x)=x2,那么函数y=f(x)的图象与函数y=|lg x|的图象的交点共有( )
| A.10个 | B.9个 | C.8个 | D.1个 |
 的必要不充分条件,求实数a的取值范围.
的必要不充分条件,求实数a的取值范围.
 时,函数
时,函数 的图象大致是( )
的图象大致是( )