题目内容
已知椭圆C: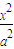 +
+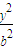 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为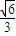 ,过右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点.
,过右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点.(1)求直线ON(O为坐标原点)的斜率KON;
(2)对于椭圆C上任意一点M,试证:总存在角θ(θ∈R)使等式:
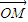 =cosθ
=cosθ +sinθ
+sinθ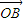 成立.
成立.
【答案】分析:(1)设出椭圆的焦距,利用离心率求得a和c的关系进而求得a和b的关系,把右焦点F的坐标代入直线AB的方程,利用韦达定理求得x1+x2的表达式,进而求得ON的斜率.
(2)根据题意可知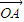 与
与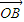 可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量
可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量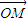 ,有且只有一对实数λ,μ,使得等式
,有且只有一对实数λ,μ,使得等式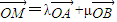 成立.设出M的坐标利用1)中各点的坐标整理求得x=λx1+μx2,y=λy1+μy2.代入椭圆的方程整理求得λ2(x12+3y12)+μ2(x22+3y22)+2λμ(x1x2+3y1y2)=3b2.利用(1)中x1+x2和x1•x2的表达式代入整理求得x1x2+3y1y2=0,进而把A,B的坐标代入椭圆的方程,联立方程求得λ2+μ2=1,设以x轴正半轴为始边,以射线OP为终边的角为θ,则可推断出λ=cosθ,μ=sinθ.进而判断出对于椭圆C上任意一点M,总存在角θ(θ∈R)使等式:
成立.设出M的坐标利用1)中各点的坐标整理求得x=λx1+μx2,y=λy1+μy2.代入椭圆的方程整理求得λ2(x12+3y12)+μ2(x22+3y22)+2λμ(x1x2+3y1y2)=3b2.利用(1)中x1+x2和x1•x2的表达式代入整理求得x1x2+3y1y2=0,进而把A,B的坐标代入椭圆的方程,联立方程求得λ2+μ2=1,设以x轴正半轴为始边,以射线OP为终边的角为θ,则可推断出λ=cosθ,μ=sinθ.进而判断出对于椭圆C上任意一点M,总存在角θ(θ∈R)使等式: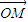 =cosθ
=cosθ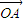 +sinθ
+sinθ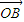 成立.
成立.
解答:解:(1)设椭圆的焦距为2c,因为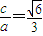 ,
,
所以有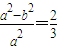 ,故有a2=3b2.从而椭圆C的方程可化为:x2+3y2=3b2①
,故有a2=3b2.从而椭圆C的方程可化为:x2+3y2=3b2①
易知右焦点F的坐标为(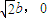 ),
),
据题意有AB所在的直线方程为: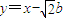 ②
②
由①,②有: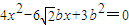 ③
③
设A(x1,y1),B(x2,y2),弦AB的中点N(x,y),由③及韦达定理有: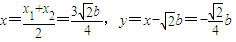 .
.
所以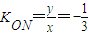 ,即为所求.
,即为所求.
(2)显然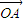 与
与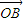 可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量
可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量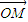 ,
,
有且只有一对实数λ,μ,使得等式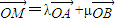 成立.
成立.
设M(x,y),由1)中各点的坐标有:(x,y)=λ(x1,y1)+μ(x2,y2),
所以x=λx1+μx2,y=λy1+μy2.
又点在椭圆C上,所以有(λx1+μx2)2+3(λy1+μy2)2=3b2
整理为λ2(x12+3y12)+μ2(x22+3y22)+2λμ(x1x2+3y1y2)=3b2.④
由③有: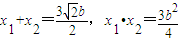 .
.
所以
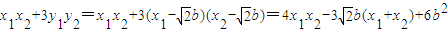
=3b2-9b2+6b2=0⑤
又A﹑B在椭圆上,故有(x12+3y12)=3b2,(x22+3y22)=3b2⑥
将⑤,⑥代入④可得:λ2+μ2=1.
对于椭圆上的每一个点M,总存在一对实数,使等式 成立,
成立,
而λ2+μ2=1
在直角坐标系x-o-y中,取点P(λ,μ),
设以x轴正半轴为始边,以射线OP为终边的角为θ,显然λ=cosθ,μ=sinθ.
也就是:对于椭圆C上任意一点M,总存在角θ(θ∈R)使等式: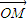 =cosθ
=cosθ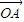 +sinθ
+sinθ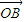 成立.
成立.
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了考生综合分析问题,基础知识的综合运用以及基本的计算能力.
(2)根据题意可知
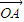 与
与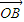 可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量
可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量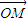 ,有且只有一对实数λ,μ,使得等式
,有且只有一对实数λ,μ,使得等式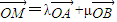 成立.设出M的坐标利用1)中各点的坐标整理求得x=λx1+μx2,y=λy1+μy2.代入椭圆的方程整理求得λ2(x12+3y12)+μ2(x22+3y22)+2λμ(x1x2+3y1y2)=3b2.利用(1)中x1+x2和x1•x2的表达式代入整理求得x1x2+3y1y2=0,进而把A,B的坐标代入椭圆的方程,联立方程求得λ2+μ2=1,设以x轴正半轴为始边,以射线OP为终边的角为θ,则可推断出λ=cosθ,μ=sinθ.进而判断出对于椭圆C上任意一点M,总存在角θ(θ∈R)使等式:
成立.设出M的坐标利用1)中各点的坐标整理求得x=λx1+μx2,y=λy1+μy2.代入椭圆的方程整理求得λ2(x12+3y12)+μ2(x22+3y22)+2λμ(x1x2+3y1y2)=3b2.利用(1)中x1+x2和x1•x2的表达式代入整理求得x1x2+3y1y2=0,进而把A,B的坐标代入椭圆的方程,联立方程求得λ2+μ2=1,设以x轴正半轴为始边,以射线OP为终边的角为θ,则可推断出λ=cosθ,μ=sinθ.进而判断出对于椭圆C上任意一点M,总存在角θ(θ∈R)使等式: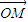 =cosθ
=cosθ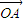 +sinθ
+sinθ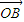 成立.
成立.解答:解:(1)设椭圆的焦距为2c,因为
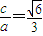 ,
,所以有
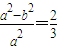 ,故有a2=3b2.从而椭圆C的方程可化为:x2+3y2=3b2①
,故有a2=3b2.从而椭圆C的方程可化为:x2+3y2=3b2①易知右焦点F的坐标为(
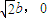 ),
),据题意有AB所在的直线方程为:
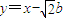 ②
②由①,②有:
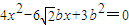 ③
③设A(x1,y1),B(x2,y2),弦AB的中点N(x,y),由③及韦达定理有:
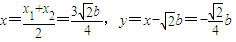 .
.所以
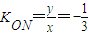 ,即为所求.
,即为所求.(2)显然
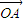 与
与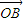 可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量
可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量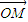 ,
,有且只有一对实数λ,μ,使得等式
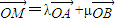 成立.
成立.设M(x,y),由1)中各点的坐标有:(x,y)=λ(x1,y1)+μ(x2,y2),
所以x=λx1+μx2,y=λy1+μy2.
又点在椭圆C上,所以有(λx1+μx2)2+3(λy1+μy2)2=3b2
整理为λ2(x12+3y12)+μ2(x22+3y22)+2λμ(x1x2+3y1y2)=3b2.④
由③有:
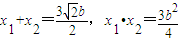 .
.所以
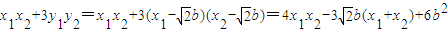
=3b2-9b2+6b2=0⑤
又A﹑B在椭圆上,故有(x12+3y12)=3b2,(x22+3y22)=3b2⑥
将⑤,⑥代入④可得:λ2+μ2=1.
对于椭圆上的每一个点M,总存在一对实数,使等式
 成立,
成立,而λ2+μ2=1
在直角坐标系x-o-y中,取点P(λ,μ),
设以x轴正半轴为始边,以射线OP为终边的角为θ,显然λ=cosθ,μ=sinθ.
也就是:对于椭圆C上任意一点M,总存在角θ(θ∈R)使等式:
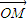 =cosθ
=cosθ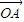 +sinθ
+sinθ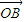 成立.
成立.点评:本题主要考查了直线与圆锥曲线的综合问题.考查了考生综合分析问题,基础知识的综合运用以及基本的计算能力.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 已知椭圆C:
已知椭圆C: +
+ =1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )
=1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )



 +
+ =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F 、F
、F ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF
 +y
+y ,y
,y =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且在x轴上的顶点分别为
,且在x轴上的顶点分别为
 :
: 与
与 轴交于点T,P为
轴交于点T,P为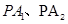 分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论. =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,短轴一
,短轴一 的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.