题目内容
设函数,则f(x)=sin(2x+
)+cos(2x+
),则( )
| π |
| 4 |
| π |
| 4 |
A、y=f(x)在(0,
| ||||
B、y=f(x)在(0,
| ||||
C、y=f(x)在(0,
| ||||
D、y=f(x)在(0,
|
分析:利用辅助角公式(两角和的正弦函数)化简函数f(x)=sin(2x+
)+cos(2x+
),然后求出对称轴方程,判断y=f(x)在(0,
)单调性,即可得到答案.
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
解答:解:因为f(x)=sin(2x+
)+cos(2x+
)=
sin(2x+
)=
cos2x.
它的对称轴方程可以是:x=
;所以A,C错误;函数y=f(x)在(0,
)单调递减,所以B错误;D正确.
故选D
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 2 |
| 2 |
它的对称轴方程可以是:x=
| π |
| 2 |
| π |
| 2 |
故选D
点评:本题是基础题,考查三角函数的化简,三角函数的性质:对称性、单调性,考查计算能力,常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
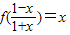 ,则f(x)的表达式( )
,则f(x)的表达式( )
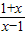


 ,则f(x)=0( )
,则f(x)=0( ) ,则f(x)的表达式( )
,则f(x)的表达式( )


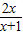
 ,则f(x)的表达式( )
,则f(x)的表达式( )


