题目内容
函数 .
.(1)如果函数f(x)在点A(2,f(2))处的切线的斜率等于3,求实数a的值;
(2)如果函数f(x)在区间[1,+∞)上无极值,求实数a的取值范围.
【答案】分析:(1)求得f'(x)=x2+ax+a2-1,根据已知条件可得f′(2)=3,可以得出a值;
(2)函数f(x)在区间[1,+∞)上无极值,分类两种情况讨论:①f′(x)=0其△≤0,②f′(x)=0其△>0,则f′(x)=0的二根应小于等于1,利用实根分布寻找关于a的不等式,求出实数a的取值范围.
解答:解:(1)由条件,f′(x)=x2+ax+a2-1,
由导数的几何意义可得f′(2)=3,解得a=0或-2;
(2)函数f(x)在区间[1,+∞)上无极值,则
①f′(x)=0其△≤0,则f(x)在R上单调递增,
则f(x)在区间[1,+∞)上无极值,解得 ;
;
②f′(x)=0其△>0,则f′(x)=0的二根应小于等于1,
由实根分布可得,

⇒ ;
;
综上, .
.
点评:本题主要考查了函数的单调性与函数导数的关系的应用,考查了一元二次方程的根的分布与系数的关系,体现了方程函数与转化思想的应用.
(2)函数f(x)在区间[1,+∞)上无极值,分类两种情况讨论:①f′(x)=0其△≤0,②f′(x)=0其△>0,则f′(x)=0的二根应小于等于1,利用实根分布寻找关于a的不等式,求出实数a的取值范围.
解答:解:(1)由条件,f′(x)=x2+ax+a2-1,
由导数的几何意义可得f′(2)=3,解得a=0或-2;
(2)函数f(x)在区间[1,+∞)上无极值,则
①f′(x)=0其△≤0,则f(x)在R上单调递增,
则f(x)在区间[1,+∞)上无极值,解得
 ;
;②f′(x)=0其△>0,则f′(x)=0的二根应小于等于1,
由实根分布可得,

⇒
 ;
;综上,
 .
.点评:本题主要考查了函数的单调性与函数导数的关系的应用,考查了一元二次方程的根的分布与系数的关系,体现了方程函数与转化思想的应用.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
 有如下性质:如果常数a>0,那么该函数在(0,
有如下性质:如果常数a>0,那么该函数在(0, ]上是减函数,在[
]上是减函数,在[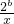 (x>0)的值域为[6,+∞),求b的值;
(x>0)的值域为[6,+∞),求b的值;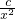 (常数c>0)在定义域内的单调性,并说明理由;
(常数c>0)在定义域内的单调性,并说明理由; (常数a>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数F(x)=
(常数a>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数F(x)=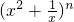 +
+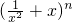 (n是正整数)在区间[
(n是正整数)在区间[ ,2]上的最大值和最小值(可利用你的研究结论).
,2]上的最大值和最小值(可利用你的研究结论).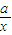 有如下性质:如果常数a>0,那么该函数在(0,
有如下性质:如果常数a>0,那么该函数在(0,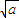 ]上是减函数,在[
]上是减函数,在[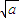 ,+∞)上是增函数.
,+∞)上是增函数.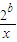 (x>0)的值域为[6,+∞),求b的值;
(x>0)的值域为[6,+∞),求b的值;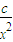 (常数c>0)在定义域内的单调性,并说明理由;
(常数c>0)在定义域内的单调性,并说明理由;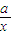 和y=x2+
和y=x2+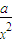 (常数a>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数F(x)=
(常数a>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数F(x)=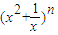 +
+ (n是正整数)在区间[
(n是正整数)在区间[ ,2]上的最大值和最小值(可利用你的研究结论).
,2]上的最大值和最小值(可利用你的研究结论). 有如下性质:如果常数a>0,那么该函数在(0,
有如下性质:如果常数a>0,那么该函数在(0, ]上是减函数,在[
]上是减函数,在[ ,+∞)上是增函数.
,+∞)上是增函数. (x>0)的值域为[6,+∞),求b的值;
(x>0)的值域为[6,+∞),求b的值; (常数c>0)在定义域内的单调性,并说明理由;
(常数c>0)在定义域内的单调性,并说明理由; 和y=x2+
和y=x2+ (常数a>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数F(x)=
(常数a>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数F(x)= +
+ (n是正整数)在区间[
(n是正整数)在区间[ ,2]上的最大值和最小值(可利用你的研究结论).
,2]上的最大值和最小值(可利用你的研究结论). 有如下性质:如果常数a>0,那么该函数在(0,
有如下性质:如果常数a>0,那么该函数在(0,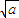 ]上是减函数,在[
]上是减函数,在[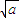 ,+∞)上是增函数.
,+∞)上是增函数.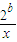 (x>0)的值域为[6,+∞),求b的值;
(x>0)的值域为[6,+∞),求b的值;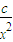 (常数c>0)在定义域内的单调性,并说明理由;
(常数c>0)在定义域内的单调性,并说明理由;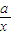 和y=x2+
和y=x2+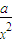 (常数a>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数F(x)=
(常数a>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数F(x)=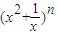 +
+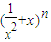 (n是正整数)在区间[
(n是正整数)在区间[ ,2]上的最大值和最小值(可利用你的研究结论).
,2]上的最大值和最小值(可利用你的研究结论).