题目内容
对于具有相同定义域D的函数f(x)和g(x),若对任意的x∈D,都有|f(x)-g(x)|≤1,则称f(x)和g(x)在D上是“密切函数”.给出定义域均为D={x|0≤x≤4}的四组函数如下:①f(x)=ln(x+1),g(x)=
 ; ②f(x)=x3,g(x)=3x-1;
; ②f(x)=x3,g(x)=3x-1;③f(x)=ex-2x(其中e为自然对数的底数),g(x)=2-x;④f(x)=
 x-
x- ,g(x)=
,g(x)= .
.其中,函数f(x)和g(x)在D上为“密切函数”的是 .
【答案】分析:对照新定义,构造新函数h(x)=f(x)-g(x),利用导数的方法确定函数的单调性,从而确定函数的值域,利用若对任意的x∈D,都有|f(x)-g(x)|≤1,则称f(x)和g(x)在D上是“密切函数”,即可得到结论
解答:解:对于①,设h(x)=f(x)-g(x)=ln(x+1)-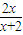 ,
,
∴ ≥0
≥0
∵0≤x≤4
∴h(x)在[0,4]上单调增,
∵h(0)=0,h(4)=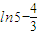
∵
∴对任意的x∈D,都有|f(x)-g(x)|≤1,
∴函数f(x)和g(x)在D上为“密切函数”;
对于②,设h(x)=f(x)-g(x)=x3-3x+1,
∴h′(x)=3x2-3
∵0≤x≤4
∴0≤x≤1,h′(x)≤0,1≤x≤4,h′(x)≥0
∵h(0)=1,h(1)=-1,h(4)=53
∴函数在x=1时,取得最小值-1;在x=4时,取得最大值53,
故不满足对任意的x∈D,都有|f(x)-g(x)|≤1;
对于③,设h(x)=f(x)-g(x)=ex-x-2,
∴h′(x)=ex-1
∵0≤x≤4
∴h′(x)≥0
∴h(x)在[0,4]上单调增,
∵h(0)=-1,h(4)=e4-6
∵e4-6>1
∴不满足对任意的x∈D,都有|f(x)-g(x)|≤1;
对于④,设h(x)=f(x)-g(x)= x-
x- -
-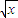 .x=0时满足题意
.x=0时满足题意
x≠0时,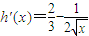
∵0<x≤4
∴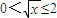
∴
∴h(x)在[0,4]上单调增,
∵h(0)=- ,h(4)=
,h(4)=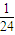
∴对任意的x∈D,都有|f(x)-g(x)|≤1,
∴函数f(x)和g(x)在D上为“密切函数”;
故答案为:①④
点评:本题是一道新定义题,要理清定义的条件和结论,将问题转化为已知的去解决,主要涉及了函数的单调性,函数的最值求法等.
解答:解:对于①,设h(x)=f(x)-g(x)=ln(x+1)-
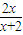 ,
,∴
 ≥0
≥0∵0≤x≤4
∴h(x)在[0,4]上单调增,
∵h(0)=0,h(4)=
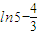
∵

∴对任意的x∈D,都有|f(x)-g(x)|≤1,
∴函数f(x)和g(x)在D上为“密切函数”;
对于②,设h(x)=f(x)-g(x)=x3-3x+1,
∴h′(x)=3x2-3
∵0≤x≤4
∴0≤x≤1,h′(x)≤0,1≤x≤4,h′(x)≥0
∵h(0)=1,h(1)=-1,h(4)=53
∴函数在x=1时,取得最小值-1;在x=4时,取得最大值53,
故不满足对任意的x∈D,都有|f(x)-g(x)|≤1;
对于③,设h(x)=f(x)-g(x)=ex-x-2,
∴h′(x)=ex-1
∵0≤x≤4
∴h′(x)≥0
∴h(x)在[0,4]上单调增,
∵h(0)=-1,h(4)=e4-6
∵e4-6>1
∴不满足对任意的x∈D,都有|f(x)-g(x)|≤1;
对于④,设h(x)=f(x)-g(x)=
 x-
x- -
-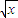 .x=0时满足题意
.x=0时满足题意x≠0时,
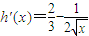
∵0<x≤4
∴
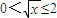
∴

∴h(x)在[0,4]上单调增,
∵h(0)=-
 ,h(4)=
,h(4)=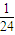
∴对任意的x∈D,都有|f(x)-g(x)|≤1,
∴函数f(x)和g(x)在D上为“密切函数”;
故答案为:①④
点评:本题是一道新定义题,要理清定义的条件和结论,将问题转化为已知的去解决,主要涉及了函数的单调性,函数的最值求法等.

练习册系列答案
相关题目