题目内容
设函数f(x)在定义域R上总有f(x)=-f(x+2),且当-1<x≤1时,f(x)=x2+2.
(1)当3<x≤5时,求函数f(x)的解析式;
(2)判断函数f(x)在(3,5]上的单调性,并予以证明.
[解析] (1)∵f(x)=-f(x+2),
∴f(x+2)=-f(x).
∴f(x)=f[(x-2)+2]=-f(x-2)=-f[(x-4)+2]=f(x-4).
∵-1<x≤1时,f(x)=x2+2,
又∵当3<x≤5时,-1<x-4≤1,
∴f(x-4)=(x-4)2+2.
∴当3<x≤5时,f(x)=(x-4)2+2.
(2)∵函数f(x)=(x-4)2+2的对称轴是x=4,
∴函数f(x)=(x-4)2+2在(3,4]上单调递减,在[4,5]上单调递增.
证明:任取x1,x2∈(3,4],且x1<x2,有
f(x1)-f(x2)
=[(x1-4)2+2]-[(x2-4)2+2]
=(x1-x2)(x1+x2-8).
∵3<x1<x2≤4,
∴x1-x2<0,x1+x2-8<0.
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
故函数y=f(x)在(3,4]上单调递减.
同理可证函数在[4,5]上单调递增.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
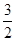 )与b=f(
)与b=f(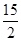 )的大小关系为____________.
)的大小关系为____________.