Question

直线y=x+1与曲线

y2

9

-

x|x|

4

=1的公共点的个数是（　　）

• A、1个
• B、2个
• C、3个
• D、4个

Answer 1

分析：由题意可得：当x≥0时，方程为

y2

9

-

x2

4

=1，其表示双曲线的一部分；当x＜0时，方程为

y2

9

+

x2

4

=1，其表示椭圆的一部分．再画出图形即可得到答案．

解答：解：由题意可得：当x≥0时，方程为

y2

9

-

x2

4

=1，其表示双曲线的一部分；当x＜0时，方程为

y2

9

+

x2

4

=1，其表示椭圆的一部分．
如图所示：

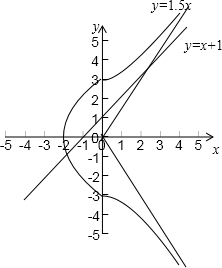
所以直线y=x+1与曲线

y2

9

-

x|x|

4

=1的公共点的个数是1．
故选A．

点评：解决此类问题的关键是熟练掌握椭圆与双曲线的图形及其画法．