题目内容
已知直线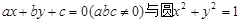 相切,则三条边长分别为|a|,|b|,|c|的三角形 。
相切,则三条边长分别为|a|,|b|,|c|的三角形 。
A.是锐角三角形 B.是直角三角形 C.是钝角三角形 D.不存在
【答案】
B
【解析】本题考查三角形分类、直线和圆的位置关系及其有关的运算.
解法一:由于直线与圆相切则有:圆心到直线的距离等于半径即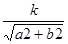 =1
=1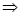 |a|2+
|a|2+
|b|2=|c|2,∴为Rt△,选B..
解法二:圆心坐标为(0,0),半径为1,因为直线和圆相切,利用点到直线距离公式得:d=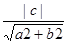 =1,即a2+b2=c2,所以,以|a|、|b|、|c|为边的三角形是直角三角形.∴选B.
=1,即a2+b2=c2,所以,以|a|、|b|、|c|为边的三角形是直角三角形.∴选B.

练习册系列答案
相关题目
 相切,则a的取值范围是( )
相切,则a的取值范围是( ) B.
B.
 或
或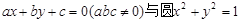 相切,则三条边长分别为|a|,|b|,|c|的三角形
。
相切,则三条边长分别为|a|,|b|,|c|的三角形
。
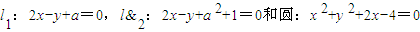 相切,则a的取值范围是( )
相切,则a的取值范围是( )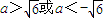
 或
或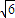 ≤a≤7
≤a≤7