题目内容
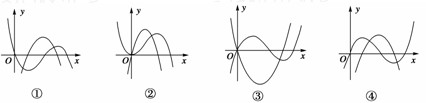
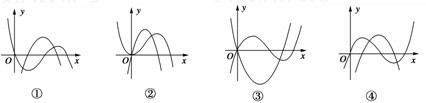
下面四图都是在同一坐标系中某三次函数及其导函数的图象,其中一定不正确的序号是
- A.①②
- B.③④
- C.①③
- D.②④
B
分析:利用导数与函数之间的关系.把握住导数的正负确定出函数的单调区间,根据变化趋势选出不恰当的图象.利用排除法确定出答案.
解答:解:根据f′(x)>0时,y=f(x)递增;f′(x)<0时,y=f(x)递减可得.③④中函数的图象的增减趋势与导函数的正负区间是吻合的,可能正确;
而②中导函数为负的区间内相应的函数不为递减,故错误,①中导函数为负的区间内相应的函数不为递减,故错误.
故选B.
分析:利用导数与函数之间的关系.把握住导数的正负确定出函数的单调区间,根据变化趋势选出不恰当的图象.利用排除法确定出答案.
解答:解:根据f′(x)>0时,y=f(x)递增;f′(x)<0时,y=f(x)递减可得.③④中函数的图象的增减趋势与导函数的正负区间是吻合的,可能正确;
而②中导函数为负的区间内相应的函数不为递减,故错误,①中导函数为负的区间内相应的函数不为递减,故错误.
故选B.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
下面四图都是在同一坐标系中某三次函数及其导函数的图象,其中一定不正确的序号是
| A.①② | B.③④ | C.①③ | D.②④ |