题目内容
设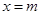 和
和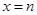 是函数
是函数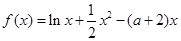 的两个极值点,其中
的两个极值点,其中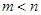 ,
,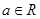 .
.
(Ⅰ) 求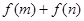 的取值范围;
的取值范围;
(Ⅱ) 若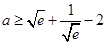 ,求
,求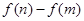 的最大值(e是自然对数的底数).
的最大值(e是自然对数的底数).
【答案】
(Ⅰ) 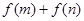 的取值范围是
的取值范围是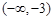 .(Ⅱ)
.(Ⅱ) 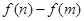 的最大值是
的最大值是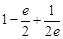 .
.
【解析】
试题分析:(Ⅰ)函数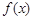 的定义域为
的定义域为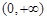 ,
,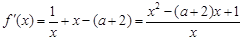 .因为
.因为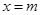 和
和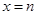 是函数
是函数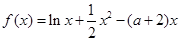 的两个极值点,所以
的两个极值点,所以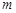 、
、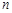 就是方程
就是方程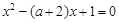 有两个不等的正根(其中
有两个不等的正根(其中 ).由此可求得
).由此可求得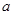 的范围故,并且可找到
的范围故,并且可找到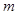 、
、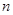 与
与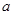 之间的关系,从而
之间的关系,从而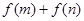 可以用
可以用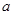 表示出来,这样根据
表示出来,这样根据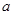 的范围便可求出
的范围便可求出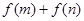 的范围.
的范围.
(Ⅱ) 首先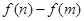 是怎样的一个式子?
是怎样的一个式子?
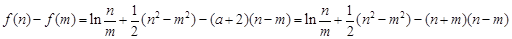 .
.
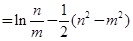 .这个式子中的
.这个式子中的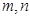 都是变量,能否变成一个?
都是变量,能否变成一个?
由题设可得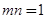 ,这样
,这样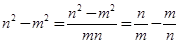 ,由此可
,由此可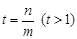 令,从而
令,从而
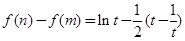 .接下来就根据
.接下来就根据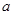 的范围求出
的范围求出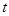 的范围,进而求出
的范围,进而求出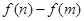 的范围.
的范围.
试题解析:(Ⅰ)函数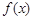 的定义域为
的定义域为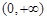 ,
,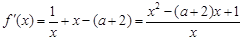 . 1分
. 1分
依题意,方程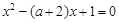 有两个不等的正根
有两个不等的正根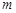 ,
,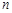 (其中
(其中 ).故
).故
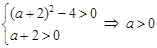 ,
3分
,
3分
并且 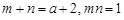 .
.
所以,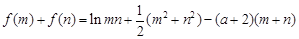
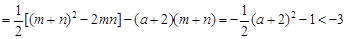
故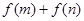 的取值范围是
的取值范围是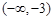 .
6分
.
6分
(Ⅱ)解:当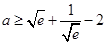 时,
时,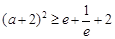 .若设
.若设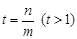 ,则
,则
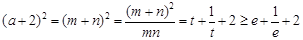 .
.
于是有 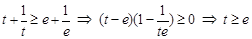
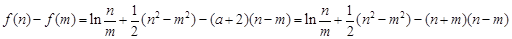
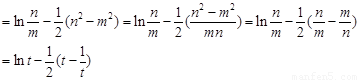
构造函数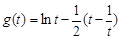 (其中
(其中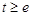 ),则
),则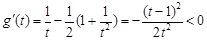 .
.
所以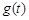 在
在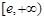 上单调递减,
上单调递减,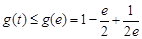 .
.
故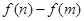 的最大值是
的最大值是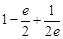 .
14分
.
14分
考点:1、导数的应用;2、不等关系.

练习册系列答案
相关题目
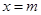 和
和 是函数
是函数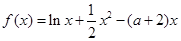 的两个极值点,其中
的两个极值点,其中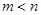 ,
,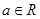 .
.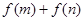 的取值范围;
的取值范围;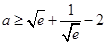 ,求
,求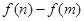 的最大值.注:e是自然对数的底.
的最大值.注:e是自然对数的底.