题目内容
(本小题满分12分)
求函数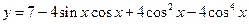 的最大值与最小值。
的最大值与最小值。
求函数
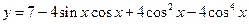 的最大值与最小值。
的最大值与最小值。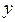 取得最大值
取得最大值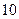 ,
,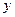 取得最小值
取得最小值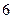
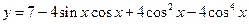
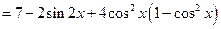
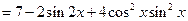
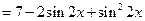
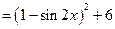
由于函数
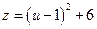 在
在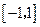 中的最大值为
中的最大值为 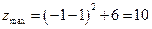
最小值为
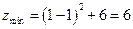
故当
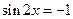 时
时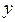 取得最大值
取得最大值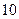 ,当
,当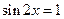 时
时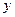 取得最小值
取得最小值
【点评】:此题重点考察三角函数基本公式的变形,配方法,符合函数的值域及最值;
【突破】:利用倍角公式降幂,利用配方变为复合函数,重视复合函数中间变量的范围是关键;

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
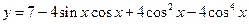 的最大值与最小值。
的最大值与最小值。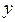 取得最大值
取得最大值 ,
,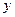 取得最小值
取得最小值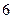
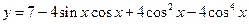
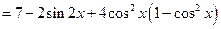
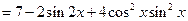
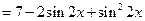
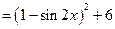
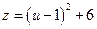 在
在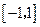 中的最大值为
中的最大值为 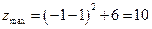
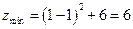
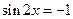 时
时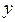 取得最大值
取得最大值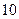 ,当
,当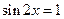 时
时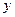 取得最小值
取得最小值

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案