题目内容
设{an}为等比数例,Tn=na1+(n-1)a2…+2an-1+an,已知T1=1,T2=4,(1)求数列{an}的首项和公比;
(2)求数列{Tn}的通项公式.
【答案】分析:(1)根据题意,首先设出等比数列的公比为q,利用题中已知的式子表示出T1,T2,又根据T1=1,T2=4,进而求出答案.
(2)根据等比数列的求和公式推出Tn的通项公式即可.
解答:解:(1)设等比数列{an}以比为q,则T1=a1,T2=2a1+a2=a1(2+q).
∵T1=1,T2=4,
∴a1=1,q=2.
(2)设Sn=a1+a2+…+an.
由(1)知an=2n-1.
∴Sn=1+2+…+2n-1
=2n-1
∴Tn=na1+(n-1)a2+…+2an-1+an
=a1+(a1+a2)+…+(a1+a2+…+an-1+an)
=S1+S2+…+Sn
=(2+1)+(2n-1)+…+(2n-1)
=(2+2n+…+2n)-n
=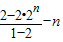
=2n+1-2-n
点评:本小题主要考查等比数列的基础知识和基本技能,运算能力.
(2)根据等比数列的求和公式推出Tn的通项公式即可.
解答:解:(1)设等比数列{an}以比为q,则T1=a1,T2=2a1+a2=a1(2+q).
∵T1=1,T2=4,
∴a1=1,q=2.
(2)设Sn=a1+a2+…+an.
由(1)知an=2n-1.
∴Sn=1+2+…+2n-1
=2n-1
∴Tn=na1+(n-1)a2+…+2an-1+an
=a1+(a1+a2)+…+(a1+a2+…+an-1+an)
=S1+S2+…+Sn
=(2+1)+(2n-1)+…+(2n-1)
=(2+2n+…+2n)-n
=
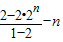
=2n+1-2-n
点评:本小题主要考查等比数列的基础知识和基本技能,运算能力.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目