题目内容
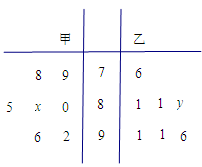
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.

(1)在乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的2个至多一个“成绩优秀”的概率;
(2)由以上统计数据填写下面列联表,并判断是否有90%的把握认为:“成绩优秀”与教学方式有关.
| | 甲班 (A方式) | 乙班 (B方式) | 总计 |
| 成绩优秀 | | | |
| 成绩不优秀 | | | |
| 总计 | | | |
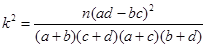
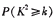 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2. 706 | 3. 841 | 5. 024 |
(1)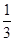 (2)列联表见解析,有90%的把握认为:“成绩优秀”与教学方式有关
(2)列联表见解析,有90%的把握认为:“成绩优秀”与教学方式有关
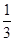 (2)列联表见解析,有90%的把握认为:“成绩优秀”与教学方式有关
(2)列联表见解析,有90%的把握认为:“成绩优秀”与教学方式有关试题分析:(1)记抽出的2个至多一个“成绩优秀”为事件A,则
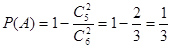
故抽出的2个至多一个“成绩优秀”的概率为
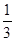 . 4分
. 4分(2) 列联表为
| | 甲班 (A方式) | 乙班 (B方式) | 总计 |
| 成绩优秀 | 1 | 5 | 6 |
| 成绩不优秀 | 19 | 15 | 34 |
| 总计 | 20 | 20 | 40 |
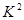 的观测值
的观测值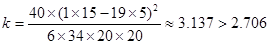 , 12分
, 12分因为
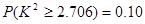
所以有90%的把握认为:“成绩优秀”与教学方式有关. 13分
点评:求解随机事件的概率要灵活运用排列组合运算公式,解决独立性检验时要注意回答的准确性.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
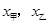 ,则下列正确的是( )
,则下列正确的是( )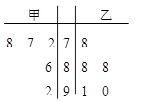
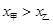 ;乙比甲成绩稳定
;乙比甲成绩稳定 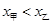 ;乙比甲成绩稳定
;乙比甲成绩稳定 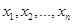 的平均数是
的平均数是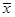 ,方差是
,方差是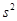 ,则另一组
,则另一组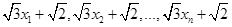 的平均数和方差分别是
的平均数和方差分别是 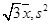
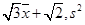
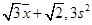
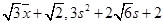
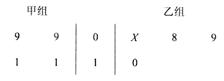
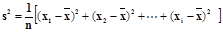 )
) 个;
个; 个;
个; 个;
个; 个;
个; 个;
个; 个。则样本在区间
个。则样本在区间 上的频率为
上的频率为 与
与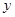 之间的一组数据如下,则
之间的一组数据如下,则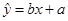 必过点
必过点 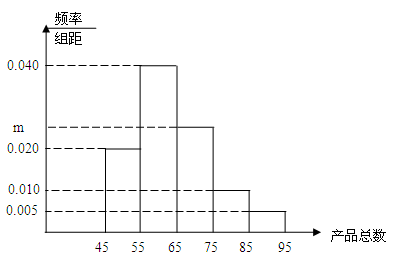


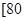 ,
,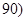 之间的矩形的高,并完成直方图;
之间的矩形的高,并完成直方图;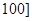 之间任取两份进行分析,在抽取的结果中,求至少有一份分数在
之间任取两份进行分析,在抽取的结果中,求至少有一份分数在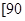 ,
,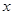
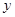 的值为
的值为