题目内容
若实数x,y满足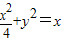 ,则x2+y2有( )
,则x2+y2有( )A.最小值
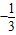 ,无最大值
,无最大值B.最小值
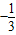 ,最大值16
,最大值16C.最小值0,无最大值
D.最小值0,最大值16
【答案】分析:从已知等式中将y用x表示出,但要注意y2≥0对应的x的范围;代入研究的代数式,得到关于x的二次函数,求出二次函数的对称轴,判断出对称轴与定义域的位置关系,得到二次函数的单调性.
解答:解:∵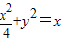
∴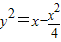 且由
且由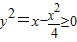 得0≤x≤4
得0≤x≤4
∴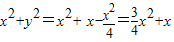 (0≤x≤4)
(0≤x≤4)
对称轴为
所以 在[0,4}上递增
在[0,4}上递增
所以当x=0时,最小为0;当x=4时最大为16
故选D
点评:本题考查等量代换的方法,注意变量的范围;考查二次函数最值的求法,关键是弄清对称轴与区间的位置关系,判断出二次函数的单调性.
解答:解:∵
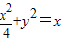
∴
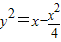 且由
且由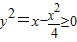 得0≤x≤4
得0≤x≤4∴
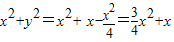 (0≤x≤4)
(0≤x≤4)对称轴为

所以
 在[0,4}上递增
在[0,4}上递增所以当x=0时,最小为0;当x=4时最大为16
故选D
点评:本题考查等量代换的方法,注意变量的范围;考查二次函数最值的求法,关键是弄清对称轴与区间的位置关系,判断出二次函数的单调性.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 ,则
,则 的取值范围是
的取值范围是  ,则s=y-x的最大值是 .
,则s=y-x的最大值是 . ,则
,则 的最小值为
的最小值为 (C)2 (D)4
(C)2 (D)4