题目内容
 是两个不共线的非零向量,且
是两个不共线的非零向量,且 .
.
(1)记 当实数t为何值时,
当实数t为何值时,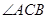 为钝角?
为钝角?
(2)令 ,求
,求 的值域及单调递减区间.
的值域及单调递减区间.
(1) ;(2)
;(2) ,
,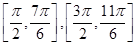
解析试题分析:(1)利用向量数量积公式可求得 ,当
,当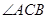 为钝角时
为钝角时 ,但
,但 时,
时, 反向,其所成角为
反向,其所成角为 ,不符合题意应舍去。(2)因为
,不符合题意应舍去。(2)因为 ,所以将
,所以将 整理成
整理成 ,属于配方法求最值。根据x的范围出
,属于配方法求最值。根据x的范围出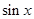 的范围,代入
的范围,代入 解析式即可求得
解析式即可求得 的值域。此函数为符合函数,根据符合函数增减口诀“同曾异减”求出其单调区间。
的值域。此函数为符合函数,根据符合函数增减口诀“同曾异减”求出其单调区间。
试题解析:(1)
 ,
, 。
。


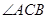 为钝角,所以
为钝角,所以 ,且
,且 。
。
当 时,
时, 即
即 ,解得
,解得 。
。
当 时,
时, 反向时,
反向时, 即
即 ,解得
,解得 ,
,
综上可得,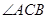 为钝角时
为钝角时
(2)

 当
当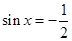 时,
时, 。当
。当 时
时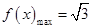 ,所以
,所以 。
。 的增区间是
的增区间是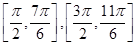
考点:向量数量积,模长,函数值域,复合函数单调性

练习册系列答案
相关题目
 中,
中,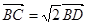 ,
, ,
, ,求
,求 的值.
的值.
 与
与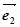 是两个单位向量,其夹角为60°,且
是两个单位向量,其夹角为60°,且 ,
,
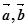 的模;
的模; sin2x+a)(x∈R,a∈R,a是常数),且y=
sin2x+a)(x∈R,a∈R,a是常数),且y= ·
· (O为坐标原点).
(O为坐标原点). ]时,f(x)的最大值为2013,求a的值.
]时,f(x)的最大值为2013,求a的值. ,求
,求 的值。
的值。 函数
函数 的第
的第 个零点记作
个零点记作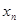 (从小到大依次计数),所有
(从小到大依次计数),所有 .
. 的值域;
的值域;  ,求数列
,求数列 .
. ,
, ,已知函数
,已知函数 在
在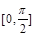 上的最大值为6.
上的最大值为6. 的值;
的值; ,
, .求
.求 的值.
的值. ,
, ,-
,- <θ<
<θ< ,求θ;
,求θ; 的最大值.
的最大值. ,
, 的值; (2)求
的值; (2)求 的夹角
的夹角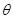 ; (3)求
; (3)求 的值;
的值;