题目内容
画出不等式|x|+|y|≤1的图形,并指出其解的范围.利用不等式的图形解不等式
①||x+1|-|x-1||<1;
②|x|+2|y|≤1.
①||x+1|-|x-1||<1;
②|x|+2|y|≤1.
分析:画出不等式|x|+|y|≤1的图形是如图所示的正方形ABCD及其内部区域,其解的范围是正方形ABCD及其内部区域的点.
①对于不等式||x+1|-|x-1||<1,根据绝对值的意义求得 ①||x+1|-|x-1||<1的解集为(-
,
).
对于不等式 ②|x|+2|y|≤1,可得|y|≤
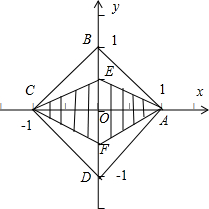
(1-|x|),其中,-1≤x≤1,它的解集是菱形AECF及其内部的点,
①对于不等式||x+1|-|x-1||<1,根据绝对值的意义求得 ①||x+1|-|x-1||<1的解集为(-
| 1 |
| 2 |
| 1 |
| 2 |
对于不等式 ②|x|+2|y|≤1,可得|y|≤
| 1 |
| 2 |
解答: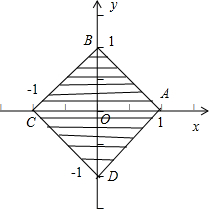 解:画出不等式|x|+|y|≤1的图形是如图所示的正方形ABCD及其内部区域,
解:画出不等式|x|+|y|≤1的图形是如图所示的正方形ABCD及其内部区域,
其解的范围是正方形ABCD及其内部区域的点.
①对于不等式||x+1|-|x-1||<1,
由于||x+1|-|x-1||表示数轴上的x对应点到-1对应点的距离减去
x对应点到1对应点的距离的绝对值,其中,-1≤x≤1.
而-
和
应点到-1对应点的距离减去它们对应点到1对应点
的距离的绝对值正好等于1,
故①||x+1|-|x-1||<1的解集为(-
,
).
对于不等式 ②|x|+2|y|≤1,可得|y|≤
(1-|x|),
其中,-1≤x≤1,它的解集是菱形AECF及其内部的点,如图所示:
 解:画出不等式|x|+|y|≤1的图形是如图所示的正方形ABCD及其内部区域,
解:画出不等式|x|+|y|≤1的图形是如图所示的正方形ABCD及其内部区域,其解的范围是正方形ABCD及其内部区域的点.
①对于不等式||x+1|-|x-1||<1,
由于||x+1|-|x-1||表示数轴上的x对应点到-1对应点的距离减去
x对应点到1对应点的距离的绝对值,其中,-1≤x≤1.
而-
| 1 |
| 2 |
| 1 |
| 2 |
的距离的绝对值正好等于1,
故①||x+1|-|x-1||<1的解集为(-
| 1 |
| 2 |
| 1 |
| 2 |
对于不等式 ②|x|+2|y|≤1,可得|y|≤
| 1 |
| 2 |
其中,-1≤x≤1,它的解集是菱形AECF及其内部的点,如图所示:

点评:本题主要考查绝对值不等式的解法,体现了数形结合的数学思想,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目