题目内容
已知光线每通过一块某种玻璃,其强度变为原来的50%.现把几块这样的玻璃重叠起来,设光线原来的强度为a,通过x块玻璃后强度为y.
(Ⅰ)写出y关于x的函数关系式,并注明定义域;
(Ⅱ)至少通过多少块玻璃后,光线强度减弱到原来的1%以下?
(Ⅰ)写出y关于x的函数关系式,并注明定义域;
(Ⅱ)至少通过多少块玻璃后,光线强度减弱到原来的1%以下?
分析:(1)由题设条件得到y=a(50%)x=a(
)x,x∈N*.
(2)由y=a(50%)x=a(
)x<a•1%,知(
)x<
,由此能求出至少通过7块玻璃后,光线强度减弱到原来的1%以下.
| 1 |
| 2 |
(2)由y=a(50%)x=a(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 100 |
解答:解:(1)∵光线每通过一块某种玻璃,其强度变为原来的50%.
现把几块这样的玻璃重叠起来,设光线原来的强度为a,通过x块玻璃后强度为y.
∴y=a(50%)x=a(
)x,x∈N*.…(7分)
(2)∵y=a(50%)x=a(
)x<a•1%,
∴(
)x<
,
∵(
)7<
<(
)6,x∈N*,
∴x≥7.
答:至少通过7块玻璃后,光线强度减弱到原来的1%以下.…(14分)
现把几块这样的玻璃重叠起来,设光线原来的强度为a,通过x块玻璃后强度为y.
∴y=a(50%)x=a(
| 1 |
| 2 |
(2)∵y=a(50%)x=a(
| 1 |
| 2 |
∴(
| 1 |
| 2 |
| 1 |
| 100 |
∵(
| 1 |
| 2 |
| 1 |
| 100 |
| 1 |
| 2 |
∴x≥7.
答:至少通过7块玻璃后,光线强度减弱到原来的1%以下.…(14分)
点评:本题考查函数解析式的求法和应用,解题时要认真审题,注意数学表达式的实际意义.

练习册系列答案
相关题目
已知光线每通过一块玻璃板,光线的强度要失掉
10%,要使玻璃板的光线强度减弱到原来强度的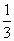 以下,则至少需要重叠玻璃板数为
以下,则至少需要重叠玻璃板数为
[
]|
A .8块 |
B .9块 |
C .10块 |
D .11块 |
已知光线每通过一块玻璃板,光线的强度要失掉10%,要使玻璃板的光线强度减弱到原来强度的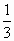 以下,则至少需要重叠玻璃板数为
以下,则至少需要重叠玻璃板数为
[ ]
|
A.8块 |
B.9块 |
C.10块 |
D.11块 |
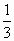 以下,则至少需要重叠玻璃板数为
以下,则至少需要重叠玻璃板数为