Question

用m，n表示两条不同的直线，α，β表示两个不同的平面，给出下列命题：
①若m⊥n，m⊥α，则n∥α；
②若m∥α，α⊥β，则m⊥β；
③若m⊥β，α⊥β，则m∥α；
④若m⊥n，m⊥α，n⊥β，则α⊥β．
其中正确命题的个数是（ ）
A．0
B．1
C．2
D．3

Answer 1

【答案】分析：利用空间直线与平面的位置关系，逐一判断．①考虑到n除了平行于α外，还有可能在α内，②画出不成立的情况说明．
③除了m平行于α外，还有可能在α内，④利用两平面垂直的判定定理证明．
解答：解：当m⊥n，m⊥α时，除了n∥α外，还有可能是n?α，∴①错误．
当m∥α，α⊥β，m与β的关系并不能确定，如右图，还可能出现m?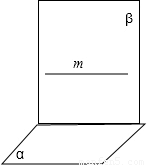β，∴②错误．
当m⊥β，α⊥β，除了m∥α外，还有可能m?α，∴③错误
当m⊥n，m⊥α时，n?α或n∥α，又∵n⊥β，∴α⊥β，④正确
故选B
点评：本题主要考查了直线，平面之间的位置关系的判断，需要学生具备空间想象力，逻辑推理能力，属于易错题．