题目内容
4.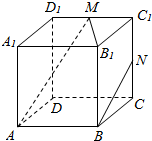 如图,正方体ABCD-A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论:
如图,正方体ABCD-A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论:①直线AM与CC1是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线AM与DD1是异面直线.
其中正确的结论为③④(注:把你认为正确的结论的序号都填上).
⑤图中正方体ABCD-A1B1C1D1的棱所在直线中与直线AB是异面直线的有4条.
分析 根据正方体的几何特征,结合已知中的图形,我们易判断出已知四个结论中的两条线段的四个端点是否共面,若四点共面,则直线可能平行或相交,反之则一定是异面直线.
解答 解:∵A、M、C、C1四点不共面
∴直线AM与CC1是异面直线,故①错误;
同理,直线AM与BN也是异面直线,故②错误.
同理,直线BN与MB1是异面直线,故③正确;
同理,直线AM与DD1是异面直线,故④正确;
正方体ABCD-A1B1C1D1的棱所在直线中与直线AB是异面直线的有CC1,DD1,A1D1,B1C1共4条,
故答案为:③④,
点评 本题考查的知识点是空间中直线与直线之间的位置关系判断,其中判断两条线段的四个顶点是否共面,进而得到答案,是解答本题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
15.函数y=ax-1+1恒过定点( )
| A. | (2,1) | B. | (1,2) | C. | (0,1) | D. | (-1,1) |
12.数列{an}前n项和为Sn,a1=1,a2=3,且an+2=|an+1-an|(n∈N*),则S2015=( )
| A. | 1342 | B. | 1344 | C. | 1346 | D. | 1348 |
16.已知点O在△ABC内部一点,且满足2$\overrightarrow{OA}$+3$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$\overrightarrow{0}$,则三角形△AOB,△BOC,△AOC的面积之比依次为( )
| A. | 4:2:3 | B. | 2:3:4 | C. | 4:3:2 | D. | 3:4:5 |
13.已知集合U={0,1,2,3},A={0,1,2},B={2,3},则(∁UA)∩B( )
| A. | {1,3} | B. | {2,3} | C. | {3} | D. | {0,1,2,3} |
 已知向量$\overrightarrow{m}=(3sinx.\frac{\sqrt{3}}{2}cosx),\overrightarrow{n}=(cosx-\frac{\sqrt{3}}{2}sinx,3cosx)$,函数f(x)=$\overrightarrow{m}•\overrightarrow{n}$.
已知向量$\overrightarrow{m}=(3sinx.\frac{\sqrt{3}}{2}cosx),\overrightarrow{n}=(cosx-\frac{\sqrt{3}}{2}sinx,3cosx)$,函数f(x)=$\overrightarrow{m}•\overrightarrow{n}$.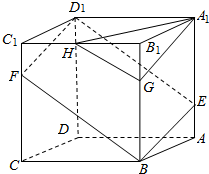 如图.已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,G在BB1上,且AE=FC1=B1G=1.H是B1C1的中点.
如图.已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,G在BB1上,且AE=FC1=B1G=1.H是B1C1的中点.