题目内容
已知函数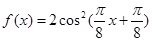 .
.
(1)把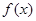 的解析式
的解析式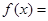 Acos(
Acos(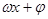 )+B的形式,并用五点法作出
)+B的形式,并用五点法作出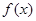 在一个周期上的简图;(要求列表)
在一个周期上的简图;(要求列表)
(2)说出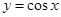 的图像经过怎样的变换
的图像经过怎样的变换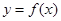 的图像.
的图像.
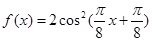 .
.(1)把
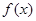 的解析式
的解析式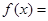 Acos(
Acos(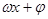 )+B的形式,并用五点法作出
)+B的形式,并用五点法作出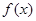 在一个周期上的简图;(要求列表)
在一个周期上的简图;(要求列表)(2)说出
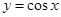 的图像经过怎样的变换
的图像经过怎样的变换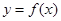 的图像.
的图像.(1)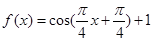 ;(2)
;(2)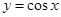 的图像向左平移
的图像向左平移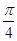 个单位得到
个单位得到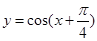 图像的;纵坐标不变,横坐标变为原来的
图像的;纵坐标不变,横坐标变为原来的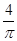 倍得到
倍得到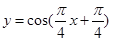 的图像;向上平移1个单位得到
的图像;向上平移1个单位得到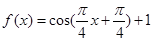 的图像.
的图像.
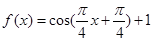 ;(2)
;(2)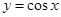 的图像向左平移
的图像向左平移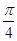 个单位得到
个单位得到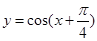 图像的;纵坐标不变,横坐标变为原来的
图像的;纵坐标不变,横坐标变为原来的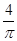 倍得到
倍得到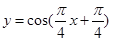 的图像;向上平移1个单位得到
的图像;向上平移1个单位得到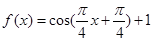 的图像.
的图像.试题分析:解题思路:(1)利用二倍角的变形“降次升角”变形即得
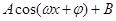 的形式,再利用“列表、描点、连线”法进行作简图;(2)利用“平移、伸缩、平移”步骤进行图像变换.规律总结:三角函数的化简,即利用同角三角函数基本关系式、诱导公式、两角和差的三角公式、二倍角公式及其变形化成
的形式,再利用“列表、描点、连线”法进行作简图;(2)利用“平移、伸缩、平移”步骤进行图像变换.规律总结:三角函数的化简,即利用同角三角函数基本关系式、诱导公式、两角和差的三角公式、二倍角公式及其变形化成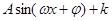 的形式;三角函数的图像变换一般两个途径:①先左右平移(左加右减),再沿横坐标轴进行伸缩(
的形式;三角函数的图像变换一般两个途径:①先左右平移(左加右减),再沿横坐标轴进行伸缩(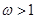 缩短,
缩短,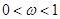 伸长),再沿纵坐标轴进行伸缩(
伸长),再沿纵坐标轴进行伸缩(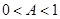 缩短,
缩短,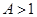 伸长).最后上下平移(上加下减);②先沿横坐标轴进行伸缩(
伸长).最后上下平移(上加下减);②先沿横坐标轴进行伸缩(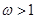 缩短,
缩短,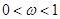 伸长),再左右平移(左加右减),再沿纵坐标轴进行伸缩(
伸长),再左右平移(左加右减),再沿纵坐标轴进行伸缩(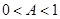 缩短,
缩短,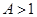 伸长).最后上下平移(上加下减).
伸长).最后上下平移(上加下减).注意点:先伸缩后平移时,要注意平移的单位
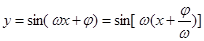 的图像由
的图像由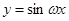 向左或右平移
向左或右平移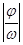 个单位.
个单位.试题解析:(1)
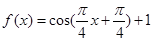 .
.列表如下:
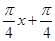 | 0 | 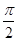 | 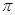 | 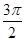 | 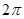 |
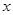 | -1 | 1 | 3 | 5 | 7 |
 | 2 | 1 | 0 | 1 | 2 |
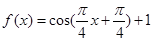 的简图如下:
的简图如下: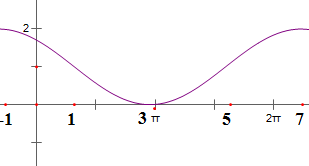
(2)
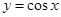 的图像向左平移
的图像向左平移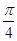 个单位得到
个单位得到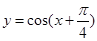 图像的;纵坐标不变,横坐标变为原来的
图像的;纵坐标不变,横坐标变为原来的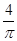 倍得到
倍得到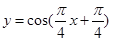 的图像;向上平移1个单位得到
的图像;向上平移1个单位得到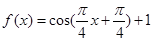 的图像.
的图像.
练习册系列答案
相关题目
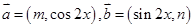 ,函数
,函数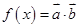 ,且
,且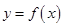 的图像过点
的图像过点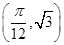 和点
和点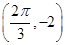 .
. 的值;
的值;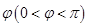 个单位后得到函数
个单位后得到函数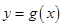 的图像,若
的图像,若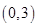 的距离的最小值为1,求
的距离的最小值为1,求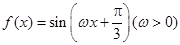 的最小正周期为
的最小正周期为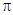 ,则该函数的图象( )
,则该函数的图象( )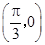 对称
对称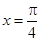 对称
对称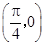 对称
对称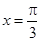 对称
对称 的对称中心为 .
的对称中心为 .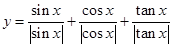 的值域为
的值域为

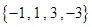

 在直线
在直线 上,则
上,则
 的最小正周期为 。
的最小正周期为 。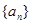 满足
满足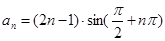 ,则它的前
,则它的前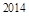 项和等于( )
项和等于( )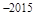
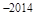
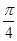 个单位长度,再将所得图象的所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的函数解析式为( ).
个单位长度,再将所得图象的所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的函数解析式为( ).