题目内容
已知两直线l1:mx+8y+n=0和l2:2x+my-1=0.试确定m、n的值,分别使
(1)l1与l2相交于点P(m,-1);
(2)l1∥l2;
(3)l1⊥l2且l1在y轴上的截距为-1.
(1)l1与l2相交于点P(m,-1);
(2)l1∥l2;
(3)l1⊥l2且l1在y轴上的截距为-1.
(1)m=1,n=7;(2)m=4,n≠-2时或m=-4,n≠2;(3)m=0且n=8.
(1)根据点P分别在直线l1和直线l2上,代入这两条直线方程,解方程组即可求得m,n.
(2)由 l1∥l2可得m·m-8×2=0得m=±4,然后分别代入检验排除掉两直线重合的情况
(3)由l1⊥l2可知m·2+8·m=0,从而求得m,然后再根据l1在y轴上的截距求得n.
解:(1)∵m2-8+n=0且2m-m-1=0,
∴m=1,n=7.
(2)由m·m-8×2=0得m=±4.
由8×(-1)-n·m≠0得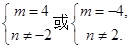
即m=4,n≠-2时或m=-4,n≠2时,l1∥l2.
(3)当且仅当m·2+8·m=0,即m=0时,
l1⊥l2,又-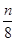 =-1,
=-1,
∴n=8.故当m=0且n=8时满足条件.
(2)由 l1∥l2可得m·m-8×2=0得m=±4,然后分别代入检验排除掉两直线重合的情况
(3)由l1⊥l2可知m·2+8·m=0,从而求得m,然后再根据l1在y轴上的截距求得n.
解:(1)∵m2-8+n=0且2m-m-1=0,
∴m=1,n=7.
(2)由m·m-8×2=0得m=±4.
由8×(-1)-n·m≠0得
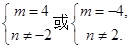
即m=4,n≠-2时或m=-4,n≠2时,l1∥l2.
(3)当且仅当m·2+8·m=0,即m=0时,
l1⊥l2,又-
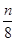 =-1,
=-1,∴n=8.故当m=0且n=8时满足条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
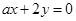 与直线
与直线 垂直,则
垂直,则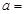
 2
2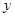 轴上的截距为
轴上的截距为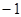 的直线方程是 ( )
的直线方程是 ( )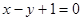
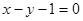
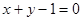
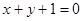
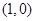 且与直线
且与直线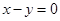 垂直的直线方程是
垂直的直线方程是 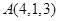 、
、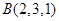 、
、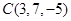 ,点
,点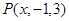 在平面
在平面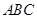 内,则实数
内,则实数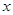 的值为( )
的值为( )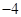
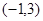 且垂直于直线
且垂直于直线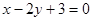 的直线方程为________.
的直线方程为________.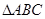 的三内角
的三内角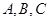 所对边的长分别为
所对边的长分别为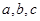 ,若直线
,若直线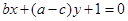 与直线
与直线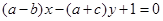 垂直,则角
垂直,则角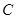 的大小为( )
的大小为( )
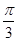
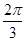
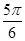
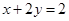 与
与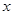 轴,
轴,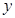 轴分别交于
轴分别交于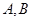 两点,若动点
两点,若动点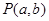 在线段
在线段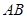 上,则
上,则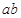 的最大值为 ( )
的最大值为 ( )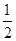
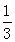
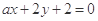 与直线
与直线 平行,那么系数
平行,那么系数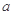 等于( )
等于( )