题目内容
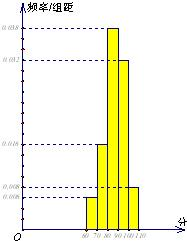 某班50名学生在一模数学考试中,成绩都属于区间[60,110].将成绩按如下方式分成五组:
某班50名学生在一模数学考试中,成绩都属于区间[60,110].将成绩按如下方式分成五组:第一组[60,70);第二组[70,80);第三组[80,90);第四组[90,100);第五组[100,110].
部分频率分布直方图如图所示,及格(成绩不小于90分)的人数为20.
(1)在成绩属于[70,80)∪[90,100]的学生中任取两人,成绩记为m,n,求|m-n|>10的概率;
(2)在该班级中任取4人,其中及极格人数记为随机变量X,写出X的分布列(结果只要求用组合数表示),并求出期望E(X).
分析:(1)欲求“|m-n|>10的概率”,即两人的分差大于10,可根据直方图得出分别在[70,80)和[90,100]中的人数,再求出在这两个区间中各取一人的方法数,利用组合数解决即可;
(2)依据及格人数X的可能值是以0,1,2,3,4,分别求出它们的概率得分布列,再根据期望的公式,代入其公式求解.
(2)依据及格人数X的可能值是以0,1,2,3,4,分别求出它们的概率得分布列,再根据期望的公式,代入其公式求解.
解答:解:(1)由图得,成绩在[100,110]的人数为4人,
所以在[90,100)的人为16人,
所以在[90,100)的频率为0.32,
在[80,90)的频率为0.38.(2分)
∴由题得:成绩在[70,80)的有8人,
在[90,100)的为16人.
所以|m-n|>10的概率为
=
.(6分)
(2)X的分布列为:
(9分)
随机变量X服从的是M=50,N=20,n=4的超几何分布,所以期望E(X)=4×
=
.(12分)
所以在[90,100)的人为16人,
所以在[90,100)的频率为0.32,
在[80,90)的频率为0.38.(2分)
∴由题得:成绩在[70,80)的有8人,
在[90,100)的为16人.
所以|m-n|>10的概率为
| ||||
|
| 32 |
| 69 |
(2)X的分布列为:

(9分)
随机变量X服从的是M=50,N=20,n=4的超几何分布,所以期望E(X)=4×
| 20 |
| 50 |
| 8 |
| 5 |
点评:本题考查频率分布直方图的相关知识.直方图中的各个矩形的面积代表了频率,所以各个矩形面积之和为1.同时也考查了分布列及数学期望的求法,属于中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 某班50名学生在一模数学考试中,成绩都属于区间[60,110].将成绩按如下方式分成五组:第一组[60,70);第二组[70,80);第三组[80,90);第四组[90,100);第五组[100,110].部分频率分布直方图如图所示,及格(成绩不小于90分)的人数为20.
某班50名学生在一模数学考试中,成绩都属于区间[60,110].将成绩按如下方式分成五组:第一组[60,70);第二组[70,80);第三组[80,90);第四组[90,100);第五组[100,110].部分频率分布直方图如图所示,及格(成绩不小于90分)的人数为20. 50名学生在一模数学考试中,成绩都属于区间[60,110]。将成绩按如下方式分成五组:第一组[60,70);第二组[70,80);第三组[80,90);第四组[90,100);第五组[100,110]。部分频率分布直方图如图3所示,及格(成绩不小于90分)的人数为20。
50名学生在一模数学考试中,成绩都属于区间[60,110]。将成绩按如下方式分成五组:第一组[60,70);第二组[70,80);第三组[80,90);第四组[90,100);第五组[100,110]。部分频率分布直方图如图3所示,及格(成绩不小于90分)的人数为20。
 ,求
,求 的概率;
的概率;
